Problem 506 | Friction

Part (a) - Force is applied horizontally
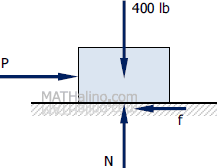
$\Sigma F_V = 0$

$N = 400 \, \text{ lb}$
 

$f = \mu N = 0.40(400)$

$f = 160 \, \text{ lb}$
 

$\Sigma F_H = 0$

$P = f$

$P = 160 \, \text{ lb}$           answer
 

Part (b) - Downward force at 30° from the horizontal
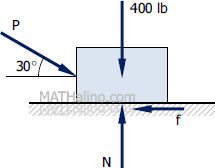$\Sigma F_V = 0$

$N = 400 + P \sin 30^\circ$

$N = 400 + 0.5P$
 

$f = \mu N = 0.40(400 + 0.5P)$

$f = 160 + 0.2P$
 

$\Sigma F_H = 0$

$P \cos 30^\circ = f$

$P \cos 30^\circ = 160 + 0.2P$

$0.666P = 160$

$P = 240.23 \, \text{ lb}$           answer
 

Another Solution for Part (b)
$\tan \phi = \mu$

$\tan \phi = 0.40$

$\phi = 21.80^\circ$
 

 

$\theta = 90^\circ - (30^\circ + \phi)$

$\theta = 90^\circ - (30^\circ + 21.80^\circ)$

$\theta = 38.20^\circ$
 

$\dfrac{P}{\sin \phi} = \dfrac{400}{\sin \theta}$

$\dfrac{P}{\sin 21.80^\circ} = \dfrac{400}{\sin 38.20^\circ}$

$P = 240.21 \, \text{ lb}$           okay!

 

Part (c) - Minimum force required to cause impending motion
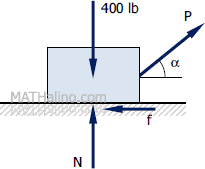$\Sigma F_V = 0$

$N = 400 - P \sin \alpha$
 

$f = \mu N = 0.40(400 - P \sin \alpha)$

$f = 160 - 0.40P \sin \alpha$
 

$\Sigma F_H = 0$

$P \cos \alpha = f$

$P \cos \alpha = 160 - 0.40P \sin \alpha$

$P \cos \alpha + 0.40P \sin \alpha = 160$

$(\cos \alpha + 0.40 \sin \alpha)P = 160$

$P = \dfrac{160}{\cos \alpha + 0.40 \sin \alpha}$
 

To minimize P, differentiate then equate to zero
$\dfrac{dP}{d\alpha} = \dfrac{-160(-\sin \alpha + 0.40 \cos \alpha)}{(\cos \alpha + 0.40 \sin \alpha)^2} = 0$

$\sin \alpha - 0.40 \cos \alpha = 0$

$\sin \alpha = 0.40 \cos \alpha$

$\tan \alpha = 0.40$

$\alpha = 21.80^\circ$
 

Minimum value of P
$P_{min} = \dfrac{160}{\cos 21.80^\circ + 0.40 \sin 21.80^\circ}$

$P_{min} = 148.56 \, \text{ lb}$           answer