Part (a) – Force P to just start the block to move up the incline
The force
P is pushing the block up the incline. The push is hard enough to overcome the maximum allowable friction causing an impending upward motion.
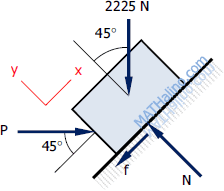 $\Sigma F_y = 0$
$\Sigma F_y = 0$
$N = 2225 \cos 45^\circ + P \sin 45^\circ$
$N = 1573.31 + 0.7071P$
$f = \mu N = 0.25(1573.31 + 0.7071P)$
$f = 393.33 + 0.1768P$
$\Sigma F_x = 0$
$P \cos 45^\circ = f + 2225 \sin 45^\circ$
$P \cos 45^\circ = (393.33 + 0.1768P) + 2225 \sin 45^\circ$
$0.5303P = 1966.64$
$P = 3708.55 \, \text{ N}$ answer
Part (b) – Force P to just prevent the block to slide down the incline
In this case, the force P is not pushing the block upward, it simply supports the block not to slide downward. Therefore, the total force that prevents the block from sliding down the plane is the sum of the component of P parallel to the incline and the upward friction force.
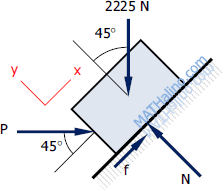 $\Sigma F_y = 0$
$\Sigma F_y = 0$
$N = 2225 \cos 45^\circ + P \sin 45^\circ$
$N = 1573.31 + 0.7071P$
$f = \mu N = 0.25(1573.31 + 0.7071P)$
$f = 393.33 + 0.1768P$
$\Sigma F_x = 0$
$P \cos 45^\circ + f = 2225 \sin 45^\circ$
$P \cos 45^\circ + (393.33 + 0.1768P) = 2225 \sin 45^\circ$
$0.8839P = 1179.98$
$P = 1335 \, \text{ N}$ answer
Part (c) – Force P = 1780 N
If Px = Wx, there will be no friction under the block. If Px > Wx, friction is going downward to help Wx balance the Px. If Px < Wx, friction is going upward to help Px balance the Wx. In this problem, the maximum available friction is not utilized by the system.
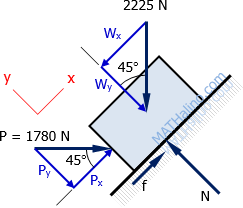 $W_x = 2225 \sin 45^\circ = 1573.31 ~ \text{N}$
$W_x = 2225 \sin 45^\circ = 1573.31 ~ \text{N}$
$P_x = 1780 \cos 45^\circ = 1258.65 ~ \text{N}$
Wx > Px, thus, f is upward.
$\Sigma F_x = 0$
$f + P_x = W_x$
$f + 1258.65 = 1573.31$
$f = 314.66 ~ \text{N upward}$ answer
