1002 Location of warning torpedo | Rectilinear Translation
Problem 1002
On a certain stretch of track, trains run at 60 mph (96.56 kph). How far back of a stopped train should be a warning torpedo be placed to signal an oncoming train? Assume that the brakes are applied at once and retard the train at the uniform rate of 2 ft/sec2 (0.61 m/s2).
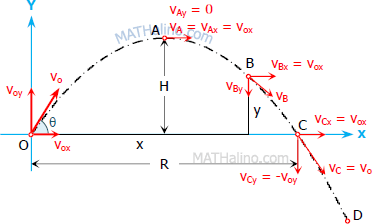
Curvilinear Translation (Projectile Motion)
Projectile motion follows a parabolic trajectory. The vertical component of projectile is under constant gravitational acceleration and the horizontal component is at constant velocity. For easy handling, resolve the motion into x and y components and use the formulas in rectilinear translation.
Form the figure below:
$v_{oy} = v_o \, \sin \theta$
- Read more about Curvilinear Translation (Projectile Motion)
- Log in to post comments
Kinematics
Motion of a Particle
Particle is a term used to denote an object of point size. A system of particles which formed into appreciable size is termed as body. These terms may apply equally to the same object. The earth for example may be assumed as a particle in comparison with its orbit, whereas to an observer on the earth, it is a body with appreciable size. In general, a particle is an object whose size is so small in comparison to the size of its path.
Rectilinear Translation (Motion Along a Straight Line)
- Read more about Kinematics
- Log in to post comments
Dynamics
Dynamics is the branch of mechanics which deals with the study of bodies in motion.
Branches of Dynamics
Dynamics is divided into two branches called kinematics and kinetics.
Kinematics is the geometry in motion. This term is used to define the motion of a particle or body without consideration of the forces causing the motion.
Kinetics is the branch of mechanics that relates the force acting on a body to its mass and acceleration.
Symbols and Notations
s = distance
- Read more about Dynamics
- Log in to post comments
820 Unsymmetrical I-section | Moment of Inertia
Problem 820
Determine the moment of inertia of the area shown in Fig. P-819 with respect to its centroidal axes.
819 Inverted T-section | Moment of Inertia
Problem 819
Determine the moment of inertia of the T-section shown in Fig. P-819 with respect to its centroidal Xo axis.
- Read more about 819 Inverted T-section | Moment of Inertia
- Log in to post comments
818 Hollow square section | Moment of Inertia and Radius of Gyration
Problem 818
A hollow square cross section consists of an 8 in. by 8 in. square from which is subtracted a concentrically placed square 4 in. by 4 in. Find the polar moment of inertia and the polar radius of gyration with respect to a z axis passing through one of the outside corners.
817 Hollow Tube | Moment of Inertia and Radius of Gyration
Problem 817
Determine the moment of inertia and radius of gyration with respect to a polar centroidal axis of the cross section of a hollow tube whose outside diameter is 6 in. and inside diameter is 4 in.
816 Polar moment of inertia and radius of gyration at one corner of rectangle
Problem 816
A rectangle is 3 in. by 6 in. Determine the polar moment of inertia and the radius of gyration with respect to a polar axis through one corner.
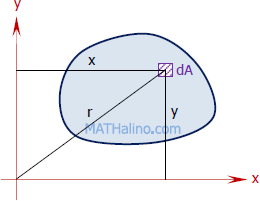
Moment of Inertia and Radius of Gyration
Moment of Inertia
Moment of inertia, also called the second moment of area, is the product of area and the square of its moment arm about a reference axis.
Moment of inertia about the x-axis:
- Read more about Moment of Inertia and Radius of Gyration
- Log in to post comments

Recent comments
(…