Problem 707 | Propped Beam with Moment Load
Problem 707
A couple M is applied at the propped end of the beam shown in Fig. P-707. Compute R at the propped end and also the wall restraining moment.

- Read more about Problem 707 | Propped Beam with Moment Load
- Log in to post comments
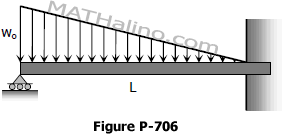
Problem 706 | Solution of Propped Beam with Decreasing Load
Example 03
The propped beam shown in Fig. P -706 is loaded by decreasing triangular load varying from wo from the simple end to zero at the fixed end. Find the support reactions and sketch the shear and moment diagrams
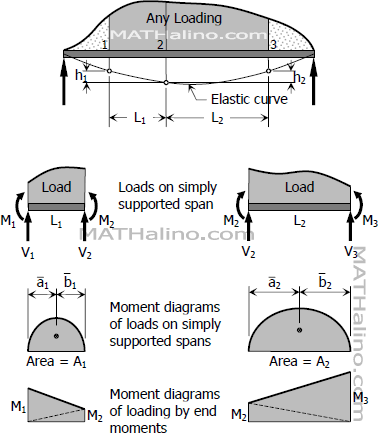
The Three-Moment Equation
The three-moment equation gives us the relation between the moments between any three points in a beam and their relative vertical distances or deviations. This method is widely used in finding the reactions in a continuous beam.
Consider three points on the beam loaded as shown.
- Read more about The Three-Moment Equation
- Log in to post comments
Continuous Beams
Continuous beams are those that rest over three or more supports, thereby having one or more redundant support reactions.
These section includes
1. Generalized form of three-moment equation
2. Factors for three-moment equation
3. Application of the three-moment equation
4. Reactions of continuous beams
5. Shear and moment diagrams of continuous beams
6. Continuous beams with fixed ends
7. Deflection determined by three-moment equation
8. Moment distribution method
- Read more about Continuous Beams
- Log in to post comments
Application of Double Integration and Superposition Methods to Restrained Beams
Superposition Method
There are 12 cases listed in the method of superposition for beam deflection.
- Cantilever beam with...
- concentrated load at the free end.
- concentrated load anywhere on the beam.
- uniform load over the entire span.
- triangular load with zero at the free end
- moment load at the free end.
- Simply supported beam with...
- concentrated load at the midspan.
- concentrated load anywhere on the beam span.
- uniform load over the entire span.
- triangular load which is zero at one end and full at the other end.
- triangular load with zero at both ends and full at the midspan.
- moment load at the right support.
- moment load at the left support.
See beam deflection by superposition method for details.
Restrained Beams
Restrained Beams
In addition to the equations of static equilibrium, relations from the geometry of elastic curve are essential to the study of indeterminate beams. Such relations can be obtained from the study of deflection and rotation of beam. This section will focus on two types of indeterminate beams; the propped beams and the fully restrained beams.
- Read more about Restrained Beams
- Log in to post comments
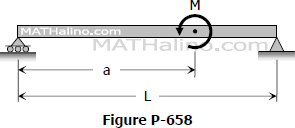
Problem 658 | Beam Deflection by Conjugate Beam Method
Problem 658
For the beam shown in Fig. P-658, find the value of EIδ at the point of application of the couple.

Recent comments
(…