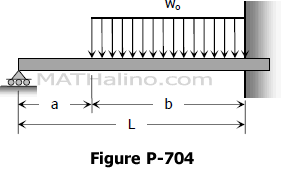
Problem 704 | Propped beam with some uniform load by moment-area method
Problem 704
Find the reaction at the simple support of the propped beam shown in Figure PB-001 by using moment-area method.
Application of Area-Moment Method to Restrained Beams
See deflection of beam by moment-area method for details.
Rotation of beam from A to B
Deviation of B from a tangent line through A
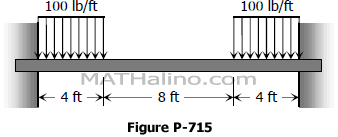
Problem 715 | Distributed loads placed symmetrically over fully restrained beam
Problem 12
Determine the moment and maximum EIδ for the restrained beam shown in Fig. RB-012. (Hint: Let the redundants be the shear and moment at the midspan. Also note that the midspan shear is zero.)
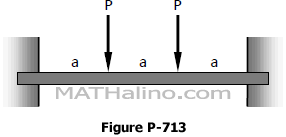
Problem 713 | Fully restrained beam with symmetrically placed concentrated loads
Problem 713
Determine the end moment and midspan value of EIδ for the restrained beam shown in Fig. PB-010. (Hint: Because of symmetry, the end shears are equal and the slope is zero at midspan. Let the redundant be the moment at midspan.)
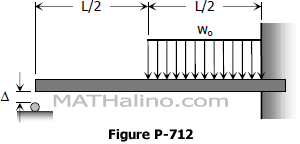
Problem 712 | Propped beam with initial clearance at the roller support
Problem 712
There is a small initial clearance D between the left end of the beam shown in Fig. P-712 and the roller support. Determine the reaction at the roller support after the uniformly distributed load is applied.
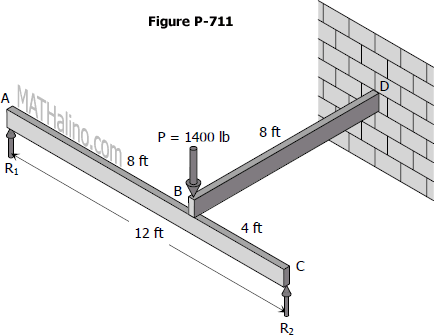
Problem 711 | Cantilever beam with free end on top of a simple beam
Problem 711
A cantilever beam BD rests on a simple beam AC as shown in Fig. P-711. Both beams are of the same material and are 3 in wide by 8 in deep. If they jointly carry a load P = 1400 lb, compute the maximum flexural stress developed in the beams.
Problem 710 | Two simple beams at 90 degree to each other
Problem 710
Two timber beams are mounted at right angles and in contact with each other at their midpoints. The upper beam A is 2 in wide by 4 in deep and simply supported on an 8-ft span; the lower beam B is 3 in wide by 8 in deep and simply supported on a 10-ft span. At their cross-over point, they jointly support a load P = 2000 lb. Determine the contact force between the beams.
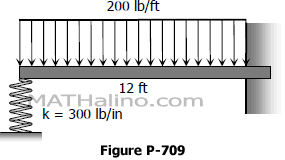
Problem 709 | Propped Beam with Spring Support
Example 06
The beam in Figure PB-006 is supported at the left by a spring that deflects 1 inch for each 300 lb. For the beam E = 1.5 × 106 psi and I = 144 in4. Compute the deflection of the spring.
- Read more about Problem 709 | Propped Beam with Spring Support
- Log in to post comments
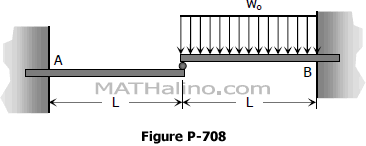
Problem 708 | Two Indentical Cantilever Beams
Problem 708
Two identical cantilever beams in contact at their ends support a distributed load over one of them as shown in Fig. P-708. Determine the restraining moment at each wall.
- Read more about Problem 708 | Two Indentical Cantilever Beams
- Log in to post comments

Recent comments
(…