02 Trapezoidal lot segregated from triangular land
Situation
A triangular lot ABC have side BC = 400 m and angle B = 50°. The lot is to be segregated by a dividing line DE parallel to BC and 150 m long. The area of segment BCDE is 50,977.4 m2.
Part 1: Calculate the area of lot ABC.
A. 62,365 m2
B. 59,319 m2
C. 57,254 m2
D. 76.325 m2
Part 2: Calculate the area of lot ADE.
A. 8,342 m2
B. 14,475 m2
C. 6,569 m2
D. 11,546 m2
Part 3: Calculate the value of angle C
A. 57°
B. 42°
C. 63°
D. 68°

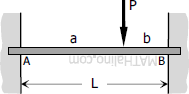 End moments
End moments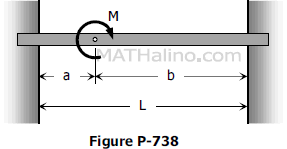
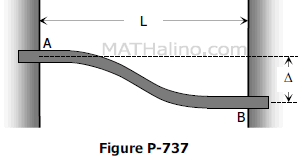
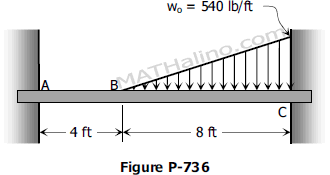
Recent comments
(…