006 Review Problem - Area illuminated by light placed in front of the globe
Problem 6
A light is placed 5 ft. from the center of the globe 3 ft. in diameter. Find the area of the illuminated portion.
 MATHalinoEngineering Math Review
MATHalinoEngineering Math ReviewProblem 6
A light is placed 5 ft. from the center of the globe 3 ft. in diameter. Find the area of the illuminated portion.
Problem 5
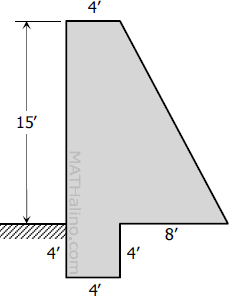
If the gravity whose cross section is shown in the figure weighs 150 lb. per cu. ft., find the total weight of a section of a dam 50 ft. long.
Problem 4
In Fingal’s Cave, on the Island of Staffa (Hebrides, Scotland), the walls are formed by basaltic prismatic columns varying in height from 18 to 36 ft. These columns, mostly hexagonal, are so perfect as to suggest the hand of man. One of the vertical columns is 29.3 ft. in height and has a base of 4.7 sq. ft. What is its volume?
Problem 3
Two spheres of lead, of radii 2 and 3 in., respectively, are melted into a cylinder of revolution of radius 1 in. Find the altitude of the cylinder.
Problem 2
The great Chinese wall is said to be 1500 miles long, 20 ft. high, 15 ft wide at the top, and 25 ft. wide at the bottom. If it were possible to build with this material a wall around the earth at the equator, of a uniform thickness of 4 ft., how high could it be made? (The equator is approximately 24,900 miles long.)
Problem 1
Find the weight of a brass water pipe 20 ft. long whose inside diameter is 1.5 in. and whose thickness is 1/4 in., if brass weighs 520 lb. per cu. ft.
| Material | Unit weight (kN/m3) |
Density (kg/m3) |
Specific Gravity |
| Aluminum | 26.095 | 2660 | 2.66 |
| Brass | 81.423 | 8300 | 8.3 |
| Brick | 19.62 | 2000 | 2.0 |
| Cast iron | 70.632 | 7200 | 7.2 |
| Concrete | 23.544 | 2400 | 2.4 |
| Copper | 87.407 | 8910 | 8.91 |
| Earth (dry) | 12.557 | 1280 | 1.28 |
| Earth (wet) | 17.266 | 1760 | 1.76 |
| Glass | 25.408 | 2590 | 2.59 |
| Ice | 8.829 | 900 | 0.9 |
| Lead | 111.540 | 11,370 | 11.37 |
| Mercury | 133.416 | 13,600 | 13.6 |
| Oil | 8.829 | 900 | 0.9 |
| Water (fresh) | 9.81 | 1000 | 1.0 |
| Water (sea) | 10.104 | 1030 | 1.03 |
| Wood (hard) | 7.848 | 800 | 0.8 |
| Wood (soft) | 4.709 | 480 | 0.48 |
Problem 422
Refer to the truss described in Problem 412 and compute the force in members BD, CD, and CE by the method of sections.

Problem 421
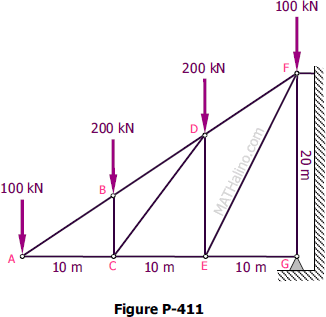
Use the method of sections to compute for the force in members DF, EF, and EG of the cantilever truss described in Problem 411 and Fig. P-411.
Problem 420
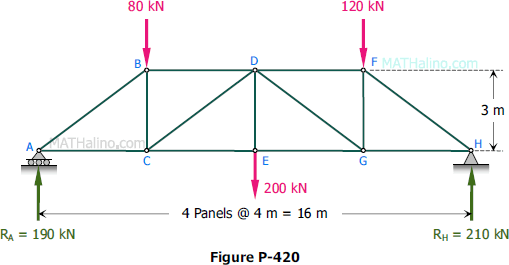
Determine the force in members DF, DG, and EG of the Howe truss shown in Fig. P-420.
Recent comments
(…