Largest parabolic section from right circular cone

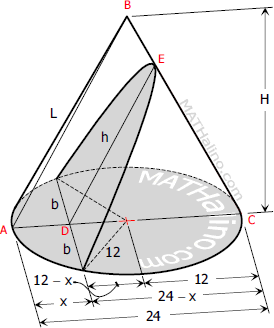
Maximum area of parabolic section
$A_{max} = \frac{2}{3}(2b)h$

$207.8 = \frac{4}{3}bh$

$h = \dfrac{155.85}{b}$   →   Equation (1)
 

Triangle DEC is similar to triangle ABC
$\dfrac{h}{24 - x} = \dfrac{L}{24}$

$h = \frac{1}{24}L(24 - x)$   →   Equation (2)
 

For the right triangle at the base of the cone
$b^2 + (12 - x)^2 = 12^2$

$b^2 = 12^2 - (12 - x)^2$

$b^2 = 12^2 - (12^2 - 24x + x^2)$

$b = \sqrt{24x - x^2}$   →   Equation (3)
 

Area of parabolic section at any distance x
$A = \frac{2}{3}(2b)h$

$A = \frac{4}{3}\sqrt{24x - x^2}[ \, \frac{1}{24}L(24 - x) \, ]$

$A = \frac{1}{18}L(24 - x)\sqrt{24x - x^2}$

$\dfrac{\partial A}{\partial x} = \frac{1}{18}L \left[ (24 - x) \dfrac{24 - 2x}{2\sqrt{24x - x^2}} + \sqrt{24x - x^2} ~ (-1) \right] = 0$

$\dfrac{2(12 - x)(24 - x)}{2\sqrt{24x - x^2}} - \sqrt{24x - x^2} = 0$

$\dfrac{(12 - x)(24 - x)}{\sqrt{24x - x^2}} = \sqrt{24x - x^2}$

$(12 - x)(24 - x) = 24x - x^2$

$288 - 36x + x^2 = 24x - x^2$

$2x^2 - 60x + 288 = 0$

$x^2 - 30x + 144 = 0$

$x = 24 \, \text{ and } \, 6$
 

Use
$x = 6 \, \text{ cm}$
 

Thus,
$b = \sqrt{24x - x^2}$   →   From Equation (3)

$b = \sqrt{24(6) - 6^2}$

$b = 6\sqrt{3} \, \text{ cm}$
 

Base-width of parabolic section
$2b = 12\sqrt{3}$

$2b = 20.78 \, \text{ cm}$           Part 1: [ D ]
 

Altitude of parabolic section
$h = \dfrac{155.85}{b}$   →   From Equation (1)

$h = \dfrac{155.85}{6\sqrt{3}}$

$h = 15 \, \text{ cm}$           Part 2: [ C ]
 

From
$h = \frac{1}{24}L(24 - x)$   →   From Equation (2)

$15 = \frac{1}{24}L(24 - 6)$

$L = 20 \, \text{ cm}$
 

By Pythagorean theorem
$H^2 + 12^2 = L^2$

$H^2 + 12^2 = 20^2$

$H = 16 \, \text{ cm}$           Part 3: [ C ]
 

Note:
For maximum area of parabola that can be cut from a right circular cone:
 

 

 

Solving the problem using the above formulas