43 - 45 Solved problems in maxima and minima

 

 

$D_1 = \sqrt{x^2 + 6^2} = \sqrt{x^2 + 36}$

$D_2 = \sqrt{(10 - x)^2 + 18^2} = \sqrt{(10 - x)^2 + 324}$
 

Total Distance:
$D = D_1 + D_2$

$D = \sqrt{x^2 + 36} + \sqrt{(10 - x)^2 + 324}$

$\dfrac{dD}{dx} = \dfrac{2x}{2\sqrt{x^2 + 36}} + \dfrac{2(10 - x)(-1)}{2 \sqrt{(10 - x)^2 + 324}} = 0$

$\dfrac{x}{\sqrt{x^2 + 36}} = \dfrac{10 - x}{\sqrt{(10 - x)^2 + 324}}$

$x\sqrt{(10 - x)^2 + 324} = (10 - x)\sqrt{x^2 + 36}$

$x^2 \, [ \, (10 - x)^2 + 324 \, ] = (10 - x)^2 \, (x^2 + 36)$

$x^2 \, (10 - x)^2 + 324x^2 = x^2 \, (10 - x)^2 + 36 (10 - x)^2$

$324x^2 = 36 (100 - 20x + x^2)$

$9x^2 = 100 - 20x + x^2$

$8x^2 + 20x - 100 = 0$

$2x^2 + 5x - 25 = 0$

$(2x - 5) (x + 5) = 0$
 

For 2x - 5 = 0; x = 5/2
For x + 5 = 0; x = -5 (meaningless)

Use x = 5/2 = 2.5 mi

 
$D = \sqrt{2.5^2 + 36} + \sqrt{(10 - 2.5)^2 + 324}$

$D = 26 \, \text{ mi}$           answer

$L_1 = \sqrt{x^2 + 8^2} = \sqrt{x^2 + 64}$
$L_2 = \sqrt{(15 - x)^2 + 12^2} = \sqrt{(15 - x)^2 + 144}$

Total length of wire:
$L = L_1 + L_2$

$L = \sqrt{x^2 + 64} + \sqrt{(15 - x)^2 + 144}$

$\dfrac{dL}{dx} = \dfrac{2x}{2\sqrt{x^2 + 64}} + \dfrac{2(15 - x)(-1)}{2\sqrt{(15 - x)^2 + 144}} = 0$

$\dfrac{x}{\sqrt{x^2 + 64}} = \dfrac{15 - x}{\sqrt{(15 - x)^2 + 144}}$

$x\sqrt{(15 - x)^2 + 144} = (15 - x)\sqrt{x^2 + 64}$

$x^2 \, [ \, (15 - x)^2 + 144 \, ] = (15 - x)^2 (x^2 + 64)$

$x^2 (15 - x)^2 + 144x^2 = x^2 (15 - x)^2 + 64 (15 - x)^2$

$144x^2 = 64 (225 - 30x + x^2)$

$9x^2 = 4 (225 - 30x + x^2)$

$5x^2 + 120x - 900 = 0$

$x^2 + 24x - 180 = 0$

$(x + 30) (x - 6) = 0$
 

For x + 30 = 0; x = -30 (meaningless)
For x - 6 = 0; x = 6 (ok)

use x = 6 ft
 

Location of stake is 6 ft from the shorter post.           answer

$S_1 = \sqrt{x^2 + a^2}$

$S_2 = \sqrt{(c - x)^2 + b^2}$
 

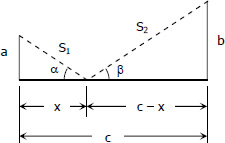Total distance traveled by light:
$S = S_1 + S_2$

$S = \sqrt{x^2 + a^2} + \sqrt{(c - x)^2 + b^2}$

$\dfrac{dS}{dx} = \dfrac{2x}{2\sqrt{x^2 + a^2}} + \dfrac{2(c - x)(-1)}{2\sqrt{(c - x)^2 + b^2}}$

$\dfrac{x}{\sqrt{x^2 + a^2}} = \dfrac{c - x}{\sqrt{(c - x)^2 + b^2}}$

$x\sqrt{(c - x)^2 + b^2} = (c - x)\sqrt{x^2 + a^2}$

$x^2 \, [ \, (c - x)^2 + b^2 \, ] = (c - x)^2 (x^2 + a^2)$

$x^2 (c - x)^2 + b^2 x^2 = x^2 (c - x)^2 + a^2 (c - x)^2$

$b^2 x^2 = a^2 (c^2 - 2cx + x^2)$

$b^2 x^2 = a^2 c^2 - 2a^2 cx + a^2 x^2$

$(a^2 - b^2)x^2 - 2a^2 cx + a^2 c^2 = 0$
 

By Quadratic Formula:
A = a² - b²; B = -2a²c; C = a²c²

$x = \dfrac{-B \pm \sqrt{B^2 - 4AC}}{2A}$

$x = \dfrac{2a^2 c \pm \sqrt{4a^4 c^2 - 4(a^2 - b^2)(a^2 c^2)}}{2(a^2 - b^2)}$

$x = \dfrac{2a^2 c \pm \sqrt{4a^4 c^2 - 4a^4 c^2 + 4 a^2 b^2 c^2}}{2(a^2 - b^2)}$

$x = \dfrac{2a^2 c \pm 2abc}{2(a^2 - b^2)}$

$x = \dfrac{ac(a \pm b)}{(a - b)(a + b)}$
 

For
$x = \dfrac{ac(a + b)}{(a - b)(a + b)}$

$x = \dfrac{ac}{a - b}$       meaningless if a > b
 

For
$x = \dfrac{ac(a - b)}{(a - b)(a + b)}$

$x = \dfrac{ac}{a + b}$       okay
 

Use
$x = \dfrac{ac}{a + b}$
 

when S is minimum:
$c - x = c - \dfrac{ac}{a + b}$

$c - x = \dfrac{(a + b)c - ac}{a + b}$

$c - x = \dfrac{ac + bc - ac}{a + b}$

$c - x = \dfrac{bc}{a + b}$
 

$\tan \alpha = \dfrac{a}{x}$

$\tan \alpha = \dfrac{a}{\dfrac{ac}{a + b}}$

$\tan \alpha = \dfrac{a + b}{c}$
 

$\tan \beta = \dfrac{b}{c - x}$

$\tan \beta = \dfrac{b}{\dfrac{bc}{a + b}}$

$\tan \beta = \dfrac{a + b}{c}$
 

tan α = tan β, thus, α = β           (okay!)