Right Circular Cone

The inside of a vase is an inverted cone 2.983 in. across the top and 5.016 in. deep. If a heavy sphere 2.498 in. in diameter is dropped into it when the vase is full of water, how much water will overflow?
 

Problem 28
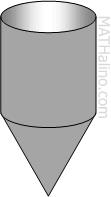A water tank, open at the top, consists of a right circular cylinder and a right circular cone, as shown. If the altitude of the cylinder is three times its radius, and the altitude of the cone is two times the same radius, find the number of square feet of sheet metal required to construct a tank having a capacity of 10,000 gal. (One gal. = 231 cu. in.)
 

Situation
A right circular cone has a base diameter of 24 cm. The maximum area of parabolic segment that can be cut from this cone is 207.8 cm².
 

Part 1: Determine the base width of the parabola.
A. 22.32 cm
B. 18.54 cm
C. 15.63 cm
D. 20.78 cm
 

Part 2: Determine the altitude of the parabola.
A. 14 cm
B. 18 cm
C. 15 cm
D. 16 cm
 

Part 2: Determine the altitude of the cone.
A. 20 cm
B. 14 cm
C. 16 cm
D. 18 cm
 

Situation
A right circular cylinder of radius r and height h is inscribed in a right circular cone of radius 6 m and height 12 m.
 

Part 1: Determine the radius of the cylinder such that its volume is a maximum.
A. 2 m
B. 4 m
C. 3 m
D. 5 m
 

Part 2: Determine the maximum volume of the cylinder.
A. 145.72 m³
B. 321.12 m³
C. 225.31 m³
D. 201.06 m³
 

Part 3: Determine the height of the cylinder such that its lateral area is a maximum.
A. 10 m
B. 8 m
C. 6 m
D. 4 m