726 Area enclosed by parabola and straigh line | Centroid of Composite Area
Problem 726
Locate the centroid of the shaded area enclosed by the curve y2 = ax and the straight line shown in Fig. P-726. Hint: Observe that the curve y2 = ax relative to the y-axis is of the form y = kx2 with respect to the x-axis.
725 Centroid of windlift of airplane wing | Centroid of area
Problem 725
Repeat Problem 239 without using integration.
724 Rectangle, semicircle, quarter-circle, and triangle | Centroid of Composite Area
Problem 724
Find the coordinates of the centroid of the shaded area shown in Fig. P-724.
723 Rectangle, quarter circle and triangle | Centroid of Composite Area
Problem 723
Locate the centroid of the shaded area in Fig. P-723.
722 Semicircle and quarter circle | Centroid of composite area
Problem 722
Locate the centroid of the shaded area in Fig. P-722 created by cutting a semicircle of diameter r from a quarter circle of radius r.
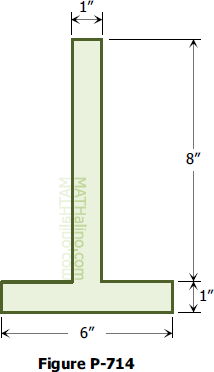
721 Increasing the width of flange to lower the centroid of inverted T-beam
Problem 721
Refer again to Fig. P-714. To what value should the 6-in. width of
the flange be changed so that the centroid of the area is 2.5 in. above the base?
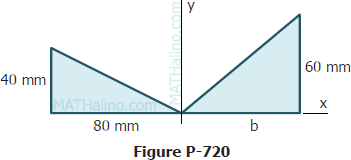
720 Two triangles | Centroid of Composite Area
Problem 720
The centroid of the sahded area in Fig. P-720 is required to lie on the y-axis. Determine the distance b that will fulfill this requirement.
- Read more about 720 Two triangles | Centroid of Composite Area
- Log in to post comments
Three-digit numbers not divisible by 3
Problem
How many three-digit numbers are not divisible by 3?
- Read more about Three-digit numbers not divisible by 3
- Log in to post comments
Variation / Proportional
Direct Variation / Directly Proportional
k = constant of proportionality
y varies directly as x is another statement equivalent to the above statement.
Inverse Variation / Directly Proportional
k = constant of proportionality
- Read more about Variation / Proportional
- Log in to post comments
Solved Problem 14 | Rectangular Parallelepiped
Problem 14
Find the angles that the diagonals of the rectangular parallelepiped 2 in. by 3 in. by 4 in. makes with the faces.
- Read more about Solved Problem 14 | Rectangular Parallelepiped
- Log in to post comments

Recent comments
(…