Derivation of Cosine Law
The following are the formulas for cosine law for any triangles with sides a, b, c and angles A, B, C, respectively.
$b^2 = a^2 + c^2 - 2ac\cos B$
$c^2 = a^2 + b^2 - 2ab\cos C$
- Read more about Derivation of Cosine Law
- Log in or register to post comments

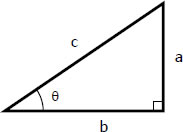 a/c = sin θ
a/c = sin θ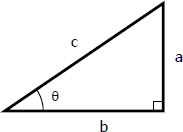 In reference to the right triangle shown and from the
In reference to the right triangle shown and from the
Recent comments