Graph of the Function y = f(x)
The graph of a function y = f(x) may be plotted using Differential Calculus. Consider the graph shown below.
 

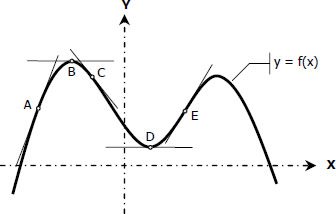
As x increases, the curve rises if the slope is positive, as of arc AB; it falls if the slope is negative, as of arc BC.
 

The sum and difference of two angles can be derived from the figure shown below.
 

Problem 569
Show that the maximum shearing stress in a beam having a thin-walled tubular section of net area A is τ = 2V / A.
 

Problem 568
Show that the shearing stress developed at the neutral axis of a beam with circular cross section is τ = (4/3)(V / π r²). Assume that the shearing stress is uniformly distributed across the neutral axis.
 

Problem 567
A timber beam 80 mm wide by 160 mm high is subjected to a vertical shear V = 40 kN. Determine the shearing stress developed at layers 20 mm apart from the top to bottom of the section.
 

Problem 564
Repeat Prob. 563 using 2-in. by 10-in. pieces.
 

Problem 563
A box beam is made from 2-in. by 6-in. pieces screwed together as shown in Fig. P-563. If the maximum flexure stress is 1200 psi, compute the force acting on the shaded portion and the moment of this force about the NA. Hint: Use the results of Prob. 562.
 

Problem 562
In any beam section having a maximum stress f_b, show that the force on any partial area A' in Fig. P-562 is given by F = (f_b/c)A'(barred y') , where (barred y') is the centroidal coordinate of A'. Also show that the moment of this force about the NA is M' = f_b I'/c, where I' is the moment of inertia of the shaded area about the NA.
 

Problem 561
A T section has the dimensions given in Fig. P-561. Show that the neutral axis is 3 inches below the top and that I_NA = 166.7 in4. If the tensile stress at the bottom of the flange is 1000 psi, calculate (a) the total tensile force in the flange and (b) the total compressive force in the cross section. Also compute (c) the moment of the compressive force about the NA, and (d) the moment of the total tensile force about the NA. (e) How does the sum of (c) and (d) compare with the total applied bending moment as computed from the flexure formula?
 

Problem 560
The wide-flange beam shown in Fig. P-560 is strengthened by bolting two cover plates 160 mm by 20 mm to the top and bottom flanges. If the maximum flexure stress is 140 MPa, compute the total force (a) in each cover plate and (b) in each flange. Neglect the weakening effect of the bolt holes.