Solution to Problem 562 | Unsymmetrical Beams

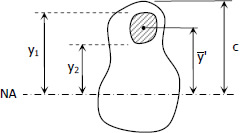
f_b = stress at c
Let
f₁ = stress at y₁
f₂ = stress at y₂
 

$f_b = \dfrac{Mc}{I}$

$M = \dfrac{f_b \, I}{c}$
 

At y₁:
$f_1 = \dfrac{My_1}{I} = \dfrac{\dfrac{f_b \, I}{c}y_1}{I}$

$f_1 = \dfrac{f_b \, y_1}{c}$
 

At y₂:
$f_2 = \dfrac{My_2}{I} = \dfrac{\dfrac{f_b \, I}{c}y_2}{I}$

$f_2 = \dfrac{f_b \, y_2}{c}$
 

At (barred y'):
$f\,' = \dfrac{f_1 + f_2}{2} = \dfrac{\dfrac{f_b \, y_1}{c} + \dfrac{f_b \, y_2}{c}}{2}$

$f\,' = \dfrac{f_b}{c} \left( \dfrac{y_1 + y_2}{2} \right)$

$f\,' = \dfrac{f_b}{c}\,\bar{y}\,'$
 

$F = f\,' \, A' = \dfrac{f_b}{c}\,\bar{y}\,' \, A'$

$F = (f_b \, / \, c) \, A' \, \bar{y}\,'$   (okay!)
 

$M = F \bar{y}\,'$

$M = [ \, (f_b \, / \, c) \, A' \, \bar{y}\,' \, ] \, \bar{y}\,'$

$M = (f_b \, / \, c) \, A' \, \bar{y}\,'^2$
 

but $\,\, A' \, \bar{y}\,'^2 = I'$
 

thus,
$M = ( \, f_b \, / \, c \, ) \, I'$

$M = f_b \, I' \, / \, c$   (okay!)