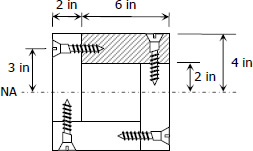
Force F acting on the shaded region
$F = ( \, f_b \, / \, c \, ) \, A' \, \bar{y} \, '$
where
$f_b = 1200 \, \text{ psi}$
$c = 4 \, \text{ in.}$
$A' = 6(2) = 12 \, \text{ in.}^2$
$\bar{y} \, ' = 3 \, \text{ in.}$
Thus,
$F = (1200/4)(12)(3)$
$F = 10 800 \, \text{lb}$
$F = 10.8 \, \text{kips}$ answer
Moment of F about the neutral axis
$M = f_b \, I' \, / \, c$
where
$I' = I + Ad^2$
$I' = \dfrac{6(2^3)}{12} + (6 \times 2)(3^2)$
$I' = 112 \, \text{in}^4$
Thus,
$M = 1200(112)/4$
$M = 33\,600 \, \text{lb}\cdot\text{in}$
$M = 2800 \, \text{lb}\cdot\text{ft}$ answer
