Solution to Problem 561 | Built-up Beams

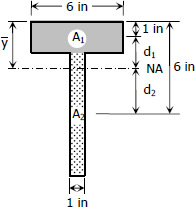
$A_1 = 6(2) = 12 \, \text{in}^2$

$A_2 = 1(8) = 8 \, \text{in}^2$

$A = A_1 + A_2 = 20 \, \text{in}^2$
 

$A \bar{y} = A_1 y_1 + A_2 y_2$

$20 \bar{y} = 12(1) + 8(6)$

$\bar{y} = 3 \, \text{m}$
 

$d_1 = y - 1 = 2 \, \text{in}$

$d_2 = 6 - y = 3 \, \text{in}$
 

$I_{NA} = (I_1 + A_1 {d_1}^2) + (I_2 + A_2 {d_2}^2)$

$I_{NA} = \left[ \dfrac{6(2^3)}{12} + 12(2^2) \right] + \left[ \dfrac{1(8^3)}{12} + 8(3^2) \right]$

$I_{NA} = 166.667 \, \text{in}^4$
 

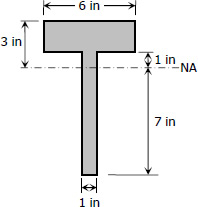$f_b = \dfrac{My}{I}$
 

At the bottom of the flange (in tension)
$100 = \dfrac{M(1)}{166.667}$

$M = 166\,667 \, \text{lb}\cdot\text{in}$
 

At the top of the flange (in tension)
$f_{bt} = \dfrac{166\,667(3)}{166.667}$

$f_{bt} = 3000 \, \text{psi}$
 

At the bottom of the section (in compression)
$f_{bc} = \dfrac{166\,667(7)}{166.667}$

$f_{bc} = 7000 \, \text{psi}$
 

(a) Total tensile force in the flange:
$F = f_{flange} A_1$
 

$f_{flange} = \dfrac{f_{bottom\,\,of\,\,flange} + f_{top\,\,of\,\,flange}}{2}$

$f_{flange} = \dfrac{1000 + 3000}{2}$

$f_{flange} = 2000 \, \text{psi}$
 

$F = 2000(12) = 24\,000 \, \text{lb}$

$F = 24 \, \text{kips} \,\, $ answer
 

(b) Total compressive force (force below NA)
$F = f_{below\,\,NA} A_{below\,\,NA}$
 

$f_{below\,\,NA} = \dfrac{f_{at\,\,NA} + f_{bottom\,\,of\,\,section}}{2}$

$f_{below\,\,NA} = \dfrac{0 + 7000}{2}$

$f_{below\,\,NA} = 3500 \, \text{psi}$

$A_{below\,\,NA} = 7(1) = 7 \, \text{in}^2$
 

$F = 3500(7) = 24\,500 \, \text{lb}$

$F = 24.5 \, \text{ kips}$           answer
 

(c) Moment of the total compressive force about NA
 

 

$M_c = F_c \,d_c = 24.5(14/3)$

$M_c = 114.3 \, \text{kip}\cdot\text{in}$
 

(d) Moment of the total tensile force
F₁ = tension force in the web

$F_1 = f_{web\,\,above\,\,NA} A_{web\,\,above\,\,NA}$
 

$f_{web\,\,above\,\,NA} = \dfrac{f_{at\,\,NA} + f_{at\,\,bottom\,\,of\,\,flange}}{2}$

$f_{web\,\,above\,\,NA} = \dfrac{0 + 100}{2} = 50 \, \text{psi}$

$A_{web\,\,above\,\,NA} = 1(1) = 1 \, \text{in}^2$
 

$F_1 = 50(1) = 50 \, \text{lb}$

$F_1 = 0.05 \, \text{kip}$

$d_1 = \frac{2}{3}(1) = \frac{2}{3} \, \text{in}$
 

F_flange = F in part (a)

F_flange = 24 kips
 

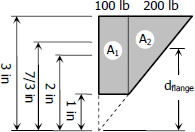$A_1 = 2(100) = 200 \, \text{lb}$

$A_2 = \frac{1}{2}(200)(2) = 200 \, \text{lb}$

$A = A_1 + A_2 = 400 \, \text{lb}$

$A \, d_{flange} = A_1(2) + A_2(7/3)$

$400d_{flange} = 200(2) + 200(7/3)$

$d_{flange} = \frac{13}{6} \, \text{in}$
 

$M_t = F_{flange}\,d_{flange} + F_1 \, d_1$

$M_t = 24(\frac{13}{6}) + 0.05(\frac{2}{3})$

$M_t = 52.03 \, \text{ kip}\cdot\text{in}$           answer