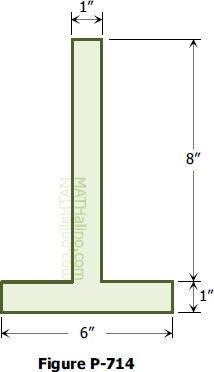
721 Increasing the width of flange to lower the centroid of inverted T-beam
Problem 721
Refer again to Fig. P-714. To what value should the 6-in. width of
the flange be changed so that the centroid of the area is 2.5 in. above the base?
Solution to Problem 572 | Horizontal Shearing Stress
Problem 572
The T section shown in Fig. P-572 is the cross-section of a beam formed by joining two rectangular pieces of wood together. The beam is subjected to a maximum shearing force of 60 kN. Show that the NA is 34 mm from the top and the INA = 10.57 × 106 mm4. Using these values, determine the shearing stress (a) at the neutral axis and (b) at the junction between the two pieces of wood.
- Read more about Solution to Problem 572 | Horizontal Shearing Stress
- Log in or register to post comments
Solution to Problem 561 | Built-up Beams
Problem 561
A T section has the dimensions given in Fig. P-561. Show that the neutral axis is 3 inches below the top and that INA = 166.7 in4. If the tensile stress at the bottom of the flange is 1000 psi, calculate (a) the total tensile force in the flange and (b) the total compressive force in the cross section. Also compute (c) the moment of the compressive force about the NA, and (d) the moment of the total tensile force about the NA. (e) How does the sum of (c) and (d) compare with the total applied bending moment as computed from the flexure formula?
- Read more about Solution to Problem 561 | Built-up Beams
- Log in or register to post comments
Solution to Problem 558 | Unsymmetrical Beams
Problem 558
In Prob. 557, find the values of x and wo so that wo is a maximum.
- Read more about Solution to Problem 558 | Unsymmetrical Beams
- Log in or register to post comments
Solution to Problem 557 | Unsymmetrical Beams
Problem 557
A cast-iron beam 10 m long and supported as shown in Fig. P-557 carries a uniformly distributed load of intensity wo (including its own weight). The allowable stresses are fbt ≤ 20 MPa and fbc ≤ 80 MPa. Determine the maximum safe value of wo if x = 1.0 m.
- Read more about Solution to Problem 557 | Unsymmetrical Beams
- Log in or register to post comments
Solution to Problem 556 | Unsymmetrical Beams
Problem 556
A T beam supports the three concentrated loads shown in Fig. P-556. Prove that the NA is 3.5 in. above the bottom and that INA = 97.0 in4. Then use these values to determine the maximum value of P so that fbt ≤ 4 ksi and fbc ≤ 10 ksi.
- Read more about Solution to Problem 556 | Unsymmetrical Beams
- Log in or register to post comments
Solution to Problem 555 | Unsymmetrical Beams
Problem 555
A beam carries a concentrated load W and a total uniformly distributed load of 4W as shown in Fig. P-555. What safe value of W can be applied if fbc ≤ 100 MPa and fbt ≤ 60 MPa? Can a greater load be applied if the section is inverted? Explain.
- Read more about Solution to Problem 555 | Unsymmetrical Beams
- Log in or register to post comments
Solution to Problem 554 | Unsymmetrical Beams
Problem 554
Determine the maximum tensile and compressive stresses developed in the overhanging beam shown in Fig. P-554. The cross-section is an inverted T with the given properties.
- Read more about Solution to Problem 554 | Unsymmetrical Beams
- Log in or register to post comments
Solution to Problem 553 | Unsymmetrical Beams
Problem 553
Determine the maximum tensile and compressive bending stresses developed in the beam as shown in Fig. P-553.
- Read more about Solution to Problem 553 | Unsymmetrical Beams
- Log in or register to post comments
Solution to Problem 552 | Unsymmetrical Beams
Problem 552
A cantilever beam carries the force and couple shown in Fig. P-552. Determine the maximum tensile and compressive bending stresses developed in the beam.
- Read more about Solution to Problem 552 | Unsymmetrical Beams
- Log in or register to post comments
