$A_1 = 9(4) = 36 \, \text{in}^2$
$A_2 = 9(1.5)(2) = 27 \, \text{in}^2$
$A_3 = 1(1.5)(2) = 3 \, \text{in}^2$
$A = A_1 - A_2 + A_3 = 36 - 27 + 3 A = 12 \, \text{in}^2$
$A \bar{y} = \Sigma A_n y$
$12\bar{y} = 36(4.5) - 27(4.5) + 3(0.5)$
$\bar{y} = 3.5 \, \text{in} \,\, $ (ok!)
$I_x = \Sigma \left( \dfrac{bh^3}{3} \right)$
$I_x = \dfrac{4(9^3)}{3} - 2 \cdot \dfrac{1.5(9^3)}{3} + 2 \cdot \dfrac{1.5(1^3)}{3}$
$I_x = 244 \, \text{in}^4$
By transfer formula for moment of inertia:
$I_x = I_{NA} + Ad^2$
$244 = I_{NA} + 12(3.5)^2$
$I_{NA} = 97 \, \text{in}^4 \,\, $ (ok!)
By symmetry:
$R_1 = R_2 = 2.5P$
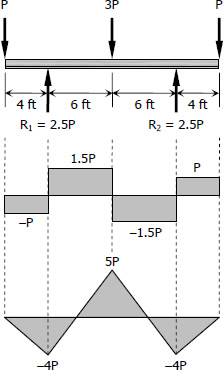$f_b = \dfrac{My}{I}$
At M = -4P lb·ft
Lower fiber is in compression:
$10 000 = \dfrac{4P(3.5)(12)}{97}$
$P = 5\,773.81 \, \text{lb}$
Upper fiber is in tension:
$4000 = \dfrac{4P(9 - 3.5)(12)}{97}$
$P = 1469.7 \, \text{lb}$
At M = 5P lb·ft
Lower fiber is in tension:
$4000 = \dfrac{4P(3.5)(12)}{97}$
$P = 1847.62 \, \text{lb}$
Upper fiber is in compression
$10\,000 = \dfrac{5P(9 - 3.5)(12)}{97}$
$P = 2939.39 \, \text{lb}$
For safe value of P, use P = 1469.7 lb answer
