Solution to Problem 557 | Unsymmetrical Beams

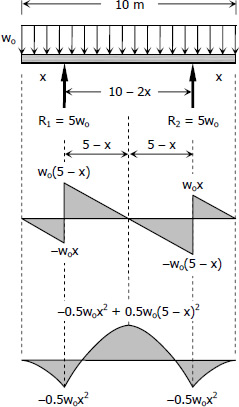
By symmetry:
$R_1 = R_2 = \frac{1}{2}(10w_o)$

$R_1 = R_2 = 5w_o$
 

$f_b = \dfrac{My}{I}$
 

At M = -0.5w_o x² N·m when x = 1 m, M = -0.5w_o N·m
 

For fiber in compression (lower)
$80 = \dfrac{0.5w_o(50)(1000)}{36 \times 10^6}$

$w_o = 115\,200 \, \text{N/m}$

$w_o = 115.2 \, \text{kN/m}$
 

For fiber in tension (upper)
$20 = \dfrac{0.5w_o(180)(1000)}{36 \times 10^6}$

$w_o = 8\,000 \, \text{N/m}$

$w_o = 8 \, \text{kN/m}$
 

At M = -0.5w_o x² + 0.5w_o(5 - x)² N·m when x = 1 m , M = 7.5w_o N·m
 

For fiber in compression (upper)
$80 = \dfrac{7.5w_o(180)(1000)}{36 \times 10^6}$

$w_o = 2\,133.33 \, \text{N/m}$

$w_o = 2.13 \, \text{kN/m}$
 

For fiber in tesnion (lower)
$20 = \dfrac{7.5w_o(50)(1000)}{36 \times 10^6}$

$w_o = 1\,920 \, \text{N/m}$

$w_o = 1.92 \, \text{kN/m}$
 

For safe load w_o, use w_o = 1.92 kN/m answer