819 Inverted T-section | Moment of Inertia
Problem 819
Determine the moment of inertia of the T-section shown in Fig. P-819 with respect to its centroidal Xo axis.
- Read more about 819 Inverted T-section | Moment of Inertia
- Log in to post comments
721 Increasing the width of flange to lower the centroid of inverted T-beam
Problem 721
Refer again to Fig. P-714. To what value should the 6-in. width of
the flange be changed so that the centroid of the area is 2.5 in. above the base?
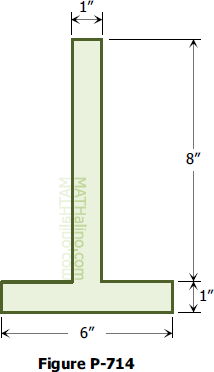
714 Inverted T-section | Centroid of Composite Figure
Problem 714
The dimensions of the T-section of a cast-iron beam are shown in Fig. P-714. How far is the centroid of the area above the base?

Solution to Problem 558 | Unsymmetrical Beams
Problem 558
In Prob. 557, find the values of x and wo so that wo is a maximum.
- Read more about Solution to Problem 558 | Unsymmetrical Beams
- Log in to post comments
Solution to Problem 557 | Unsymmetrical Beams
Problem 557
A cast-iron beam 10 m long and supported as shown in Fig. P-557 carries a uniformly distributed load of intensity wo (including its own weight). The allowable stresses are fbt ≤ 20 MPa and fbc ≤ 80 MPa. Determine the maximum safe value of wo if x = 1.0 m.
- Read more about Solution to Problem 557 | Unsymmetrical Beams
- Log in to post comments
Solution to Problem 556 | Unsymmetrical Beams
Problem 556
A T beam supports the three concentrated loads shown in Fig. P-556. Prove that the NA is 3.5 in. above the bottom and that INA = 97.0 in4. Then use these values to determine the maximum value of P so that fbt ≤ 4 ksi and fbc ≤ 10 ksi.
- Read more about Solution to Problem 556 | Unsymmetrical Beams
- Log in to post comments
Solution to Problem 554 | Unsymmetrical Beams
Problem 554
Determine the maximum tensile and compressive stresses developed in the overhanging beam shown in Fig. P-554. The cross-section is an inverted T with the given properties.
- Read more about Solution to Problem 554 | Unsymmetrical Beams
- Log in to post comments
Solution to Problem 552 | Unsymmetrical Beams
Problem 552
A cantilever beam carries the force and couple shown in Fig. P-552. Determine the maximum tensile and compressive bending stresses developed in the beam.
- Read more about Solution to Problem 552 | Unsymmetrical Beams
- Log in to post comments
Solution to Problem 548 | Unsymmetrical Beams
Problem 548
The inverted T section of a 4-m simply supported beam has the properties shown in Fig. P-548. The beam carries a uniformly distributed load of intensity wo over its entire length. Determine wo if fbt ≤ 40 MPa and fbc ≤ 80 MPa.
- Read more about Solution to Problem 548 | Unsymmetrical Beams
- Log in to post comments
