Solution to Problem 555 | Unsymmetrical Beams

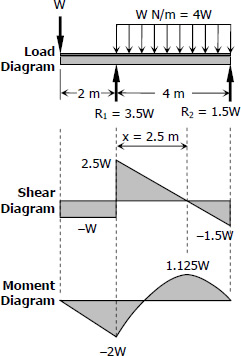
$\Sigma M_{R2} = 0$

$4R_1 = 6W + 4W(2)$

$R_1 = 3.5W$
 

$\Sigma M_{R1} = 0$

$4R_2 + 2W = 4W(2)$

$R_2 = 1.5W$
 

$\dfrac{x}{2.5W} = \dfrac{4 - x}{1.5W}$

$1.5Wx = 10W - 2.5Wx$

$x = 2.5 \, \text{m}$
 

$f_b = \dfrac{My}{I}$
 

At M = -2W
 

For lower fiber, f_bc ≤ 100 MPa
$100 = \dfrac{2W(125)(1000)}{24 \times 10^6}$

$W = 9600 \, \text{N}$
 

For upper fiber, f_bt ≤ 60 MPa
$60 = \dfrac{2W(75)(1000)}{24 \times 10^6}$

$W = 9600 \, \text{N}$
 

At M = 1.125W
 

For upper fiber, f_bc ≤ 100 MPa
$100 = \dfrac{1.125W(75)(1000)}{24 \times 10^6}$

$W = 28\,444.44 \, \text{N}$
 

For lower fiber, f_bt ≤ 60 MPa
$60 = \dfrac{1.125W(125)(1000)}{24 \times 10^6}$

$W = 10\,240 \, \text{N}$
 

For safe load W, use W = 9600 N answer
 

Discussion:
At W = 9600 N, the allowable f_b in tension and compression are reached simultaneously when M = -2W. This is the same even if the section is inverted. Therefore, no load can be applied greater than W = 9600 N.