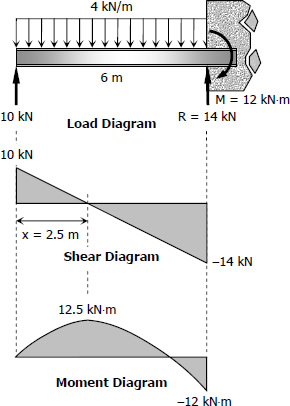
$M = 4(6)(3) - 10(6) = 12 \, \text{kN}\cdot\text{m}$
$R = 4(6) - 10 = 14 \, \text{kN}$
$\dfrac{x}{10} = \dfrac{6 - x}{14}$
$14x = 60 - 10x$
$x = 2.5 \, \text{m}$
$f_b = \dfrac{My}{I}$
At M = +12.5 kN·m
$f_{bc} = \dfrac{12.5(130)(1000^2)}{100 \times 10^6}$
$f_{bc} = 16.25 \, \text{MPa} \,\, \to \,\,$ upper fiber
$f_{bt} = \dfrac{12.5(200)(1000^2)}{100 \times 10^6}$
$f_{bt} = 25 \, \text{MPa} \,\, \to \,\,$ lower fiber
At M = -12 kN·m
$f_{bc} = \dfrac{12(200)(1000^2)}{100 \times 10^6}$
$f_{bc} = 24 \, \text{MPa} \,\, \to \,\,$ lower fiber
$f_{bt} = \dfrac{12(130)(1000^2)}{100 \times 10^6}$
$f_{bt} = 15.6 \, \text{MPa} \,\, \to \,\,$ lower fiber
Maximum flexure stresses:
fbc = 24 MPa at the fixed end answer
fbt = 25 MPa at 2.5 m from the free end answer
