$f_v = \dfrac{VQ}{Ib}$
Where
 $f_v = \tau$
$f_v = \tau$
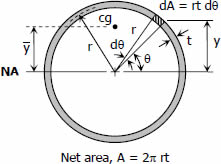
$\bar{y} = \dfrac{2r}{\pi}$
$Q = \frac{1}{2}(2 \pi rt)\left( \dfrac{2r}{\pi} \right) = 2r^2 \, t$
$dA = (r \, d\theta)t = rt \, d\theta$
$\sin \theta = \dfrac{y}{r}; \,\, y = r \sin \theta$
$\displaystyle I = \int_a^b y^2 \, dA = \int_0^{2\pi} (r^2 \sin^2 \theta)(rt \, d\theta)$
$\displaystyle I = r^3 t \int_0^{2\pi} \sin^2 \theta \, d\theta$
$\displaystyle I = r^3 t \int_0^{2\pi} \frac{1}{2} (1 - \cos 2\theta) \, d\theta$
$I = \dfrac{r^3 \, t}{2} \left[ \, \theta - \frac{1}{2} \cos 2\theta \, \right]_0^{2\pi}$
$I = \dfrac{r^3 \, t}{2} \left[ \, 2\pi - \frac{1}{2} \cos 4\pi \, \right] = \pi r^3 \, t$
$b = 2t$
Thus,
$\tau = \dfrac{V(2r^2 \, t)}{\pi r^3 \, t(2t)} = \dfrac{2Vr^2 \, t}{2\pi r^3 \, t^2} = \dfrac{2V}{2 \pi r \, t}$
$\tau = \dfrac{2V}{A}$ (ok!)
