Bolted Connection
Spacing of Bolts / Nails / Screws
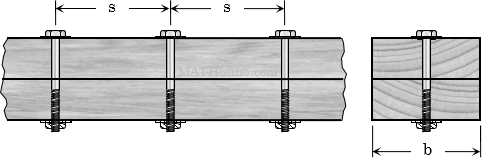
$s = \dfrac{RI}{VQ}$
$s = \dfrac{R}{q}$
- Read more about Bolted Connection
- Log in to post comments
 MATHalinoEngineering Math Review
MATHalinoEngineering Math ReviewSpacing of Bolts / Nails / Screws

$s = \dfrac{RI}{VQ}$
$s = \dfrac{R}{q}$
Problem 577
A plywood beam is built up of 1/4-in. strips separated by blocks as shown in Fig. P-577. What shearing force V will cause a maximum shearing stress of 200 psi?
Problem 576
Rework Prob. 575 assuming that the web is 200 mm instead of 160 mm.
Problem 575
Determine the maximum and minimum shearing stress in the web of the wide flange section in Fig. P-575 if V = 100 kN. Also, compute the percentage of vertical shear carried only by the web of the beam.
Problem 574
In the beam section shown in Fig. P-574, prove that the maximum horizontal shearing stress occurs at layers h/8 above or below the NA.
Problem 573
The cross-section of a beam is an isosceles triangle with vertex uppermost, of altitude h and base b. If V is the vertical shear, show that the maximum shearing stress is 3V / bh located at the midpoint of the altitude.
Problem 572
The T section shown in Fig. P-572 is the cross-section of a beam formed by joining two rectangular pieces of wood together. The beam is subjected to a maximum shearing force of 60 kN. Show that the NA is 34 mm from the top and the INA = 10.57 × 106 mm4. Using these values, determine the shearing stress (a) at the neutral axis and (b) at the junction between the two pieces of wood.
Problem 571
For a beam with the same cross section as that in Prob. 570, plot the shearing stress distribution across the section at a section where the shearing force is V = 1800 lb.
Problem 570
A uniformly distributed load of 200 lb/ft is carried on a simply supported beam span. If the cross-section is as shown in Fig. P-570, determine the maximum length of the beam if the shearing stress is limited to 80 psi. Assume the load acts over the entire length of the beam.
Problem 569
Show that the maximum shearing stress in a beam having a thin-walled tubular section of net area A is τ = 2V / A.