By symmetry
$R_A = R_H = \frac{1}{2}(3 \times 8)$
$R_A = R_H = 12 \, \text{kN}$
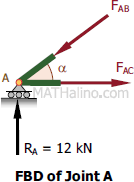 At Joint A
At Joint A
$\Sigma F_V = 0$
$F_{AB} \sin \alpha = 12$
$F_{AB} (\frac{3}{5}) = 12$
$F_{AB} = 20 \, \text{kN}$ compression
$\Sigma F_H = 0$
$F_{AC} = F_{AB} \cos \alpha�$
$F_{AC} = 20 (\frac{4}{5})$
$F_{AC} = 16 \, \text{kN}$ tension
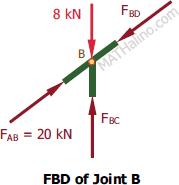 At Joint B
At Joint B
By inspection
$F_{BD} = 20 \, \text{kN}$ compression
$F_{BC} = 8 \, \text{kN}$ compression
At Joint C
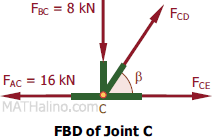 $\Sigma F_V = 0$
$\Sigma F_V = 0$
$F_{CD} \sin \beta = 8$
$F_{CD} (\frac{3}{\sqrt{13}}) = 8$
$F_{CD} = 9.6148 \, \text{kN}$ tension
$\Sigma F_H = 0$
$F_{CE} + F_{CD} \cos \beta = 16$
$F_{CE} + 9.6148(\frac{2}{\sqrt{13}}) = 16$
$F_{CE} = 10.6667 \, \text{kN}$ tension
At Joint E
By inspection
$F_{DE} = 0$
Summary
AB = FH = 20 kN compression
AC = GH = 16 kN tension
BC = FG = 8 kN compression
BD = DF = 20 kN compression
CD = DG = 9.6148 kN tension
CE = EG = 10.6667 kN tension
DE = 0

how were you able to get the
how were you able to get the triangle? the one on point A