Laplace Transform of Derivatives
For first-order derivative:
$\mathcal{L} \left\{ f'(t) \right\} = s \, \mathcal{L} \left\{ f(t) \right\} - f(0)$
For second-order derivative:
$\mathcal{L} \left\{ f''(t) \right\} = s^2 \mathcal{L} \left\{ f(t) \right\} - s \, f(0) - f'(0)$
For third-order derivative:
$\mathcal{L} \left\{ f'''(t) \right\} = s^3 \mathcal{L} \left\{ f(t) \right\} - s^2 f(0) - s \, f'(0) - f''(0)$
For nth order derivative:
- Read more about Laplace Transform of Derivatives
- Log in to post comments
Compound Interest
In compound interest, the interest earned by the principal at the end of each interest period (compounding period) is added to the principal. The sum (principal + interest) will earn another interest in the next compounding period.
Consider \$1000 invested in an account of 10% per year for 3 years. The figures below shows the contrast between simple interest and compound interest.
- Read more about Compound Interest
- Log in to post comments
Simple Interest
Simple Interest
In simple interest, only the original principal bears interest and the interest to be paid varies directly with time.
The formula for simple interest is given by
The future amount is
- Read more about Simple Interest
- Log in to post comments
Derivation of Formula for the Future Amount of Ordinary Annuity
The sum of ordinary annuity is given by
To learn more about annuity, see this page: ordinary annuity, deferred annuity, annuity due, and perpetuity.
Derivation
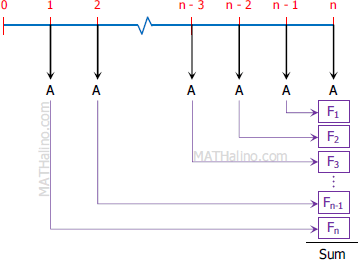
$F = \text{ Sum}$
$F = A + F_1 + F_2 + F_3 + \cdots + F_{n-1} + F_n$
$F = A + A(1 + i) + A(1 + i)^2 + A(1 + i)^3 + \cdots + A(1 + i)^{n-1} + A(1 + i)^n$

Recent comments
(…