Compound Interest

In compound interest, the interest earned by the principal at the end of each interest period (compounding period) is added to the principal. The sum (principal + interest) will earn another interest in the next compounding period.
 

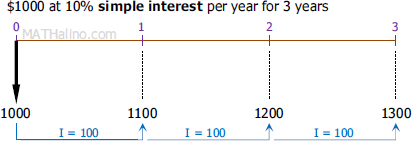
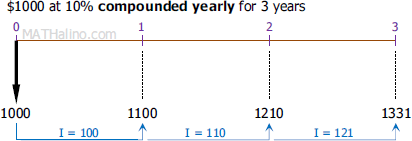
Consider $1000 invested in an account of 10% per year for 3 years. The figures below shows the contrast between simple interest and compound interest.
 

At 10% simple interest, the $1000 investment amounted to $1300 after 3 years. Only the principal earns interest which is $100 per year.
 

At 10% compounded yearly, the $1000 initial investment amounted to $1331 after 3 years. The interest also earns an interest.
 

Elements of Compound Interest
$P$ = principal, present amount
$F$ = future amount, compound amount
$i$ = interest rate per compounding period
$r$ = nominal annual interest rate
$n$ = total number of compounding in t years
$t$ = number of years
$m$ = number of compounding per year

Future amount,

The factor   $(1 + i)^n$   is called single-payment compound-amount factor and is denoted by   $(F/P, \, i, \, n)$.
 

Present amount,

The factor   $\dfrac{1}{(1 + i)^n}$   is called single-payment present-worth factor and is denoted by   $(P/F, \, i, \, n)$.
 

Number of compounding periods,

Interest rate per compounding period,

Values of   $i$   and   $n$
In most problems, the number of years   $t$   and the number of compounding periods per year   $m$   are given. The example below shows the value of   $i$   and   $n$.

Example
Number of years,   $t = 5 \text{ years}$
Nominal rate,   $r = 18\%$

• Compounded annually ($m = 1$)

  $n = 1(5) = 5$

  $i = 0.18 / 1 = 0.18$

• Compounded semi-annually ($m = 2$)

  $n = 2(5) = 10$

  $i = 0.18 / 2 = 0.09$

• Compounded quarterly ($m = 4$)

  $n = 4(5) = 20$

  $i = 0.18 / 4 = 0.045$

• Compounded semi-quarterly ($m = 8$)

  $n = 8(5) = 40$

  $i = 0.18 / 4 = 0.0225$

• Compounded monthly ($m = 12$)

  $n = 12(5) = 60$

  $i = 0.18 / 12 = 0.015$

• Compounded bi-monthly ($m = 6$)

  $n = 6(5) = 30$

  $i = 0.18 / 6 = 0.03$

• Compounded daily ($m = 360$)

  $n = 360(5) = 1800$

  $i = 0.18 / 360 = 0.0005$

Continuous Compounding (m → ∞)
In continuous compounding, the number of interest periods per year approaches infinity. From the equation
$F = \left( 1 + \dfrac{r}{m} \right)^{mt}$
 

when   $m \to \infty$,   $mt = \infty$,   and   $\dfrac{r}{m} \to 0$.   Hence,
$\displaystyle F = P \lim_{m \to \infty}\left( 1 + \dfrac{r}{m} \right)^{mt}$
 

Let   $x = \dfrac{r}{m}$.   When   $m \to \infty$,   $x \to 0$,   and   $m = \dfrac{r}{x}$.

$\displaystyle F = P \lim_{x \to 0}(1 + x)^{\frac{r}{x}t}$

$\displaystyle F = P \lim_{x \to 0}(1 + x)^{\frac{1}{x}rt}$
 

From Calculus,   $\displaystyle \lim_{x \to \infty}(1 + x)^{1/x} = e$,   thus,