Method of Sections | Analysis of Simple Trusses
Method of Sections
In this method, we will cut the truss into two sections by passing a cutting plane through the members whose internal forces we wish to determine. This method permits us to solve directly any member by analyzing the left or the right section of the cutting plane.
To remain each section in equilibrium, the cut members will be replaced by forces equivalent to the internal load transmitted to the members. Each section may constitute of non-concurrent force system from which three equilibrium equations can be written.
- Read more about Method of Sections | Analysis of Simple Trusses
- Log in or register to post comments
Problem 403 | Method of Joints
Problem 403
Determine the force in each bar of the truss shown in Fig. P-403.

- Read more about Problem 403 | Method of Joints
- Log in or register to post comments
Problem 001-mj | Method of Joints
Problem
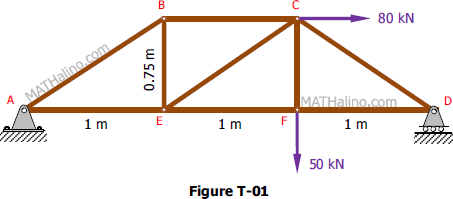
Find the force acting in all members of the truss shown in Figure T-01.
- Read more about Problem 001-mj | Method of Joints
- Log in or register to post comments
Method of Joints | Analysis of Simple Trusses
Method of Joints
The free-body diagram of any joint is a concurrent force system in which the summation of moment will be of no help. Recall that only two equilibrium equations can be written
- Read more about Method of Joints | Analysis of Simple Trusses
- Log in or register to post comments
Analysis of Structures
There are many kinds of structure. This section will limit to those that are pin-connected. Two types of pin-connected structures will be covered here; pin-connected trusses and pin-connected frames. In the actual structure, the joints may be welded, riveted, or bolted to a gusset plate at the joint. However as long as the center-line of the member coincide at the joint, the assumption of a pinned joint maybe used.
- Read more about Analysis of Structures
- Log in or register to post comments
Problem 04 | Division by t
- Read more about Problem 04 | Division by t
- Log in or register to post comments
Problem 03 | Division by t
- Read more about Problem 03 | Division by t
- Log in or register to post comments
Greek Alphabets
The following are Greek alphabets commonly used in science and mathematics.
| Greek Symbol | Greek Letter Name | English Equivalent | |
| Upper Case | Lower Case | ||
| Α | α | Alpha | a |
| Β | β | Beta | b |
| Γ | γ | Gamma | g |
| Δ | δ | Delta | d |
| Ε | ε | Epsilon | e |
| Ζ | ζ | Zeta | z |
| Η | η | Eta | h |
| Θ | θ | Theta | th |
| Ι | ι | Iota | i |
| Κ | κ | Kappa | k |
| Λ | λ | Lambda | l |
| Μ | μ | Mu | m |
| Ν | ν | Nu | n |
| Ξ | ξ | Xi | x |
| Ο | ο | Omicron | o |
| Π | π | Pi | p |
| Ρ | ρ | Rho | r |
| Σ | σ | Sigma | s |
| Τ | τ | Tau | t |
| Υ | υ | Upsilon | u |
| Φ | φ | Phi | ph |
| Χ | χ | Chi | ch |
| Ψ | ψ | Psi | ps |
| Ω | ω | Omega | o |
- Read more about Greek Alphabets
- Log in or register to post comments
Problem 02 | Division by t
- Read more about Problem 02 | Division by t
- Log in or register to post comments
Problem 01 | Division by t
- Read more about Problem 01 | Division by t
- Log in or register to post comments

Recent comments