Problem 01 | First Shifting Property of Laplace Transform
Problem 01
Find the Laplace transform of $f(t) = e^{2t}t^3$.
Problem 01
Find the Laplace transform of $f(t) = e^{2t}t^3$.
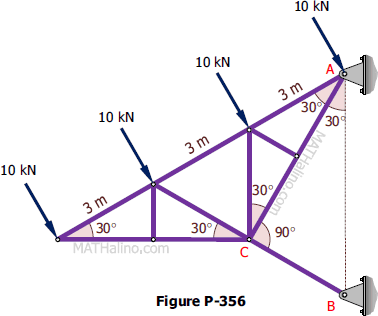
Problem 356
The cantilever truss shown in Fig. P-356 is supported by a hinge at A and a strut BC. Determine the reactions at A and B.
First Shifting Property
If $\mathcal{L} \left\{ f(t) \right\} = F(s)$, when $s > a$ then,
In words, the substitution $s - a$ for $s$ in the transform corresponds to the multiplication of the original function by $e^{at}$.
Problem 01
Find the Laplace transform of $f(t) = 5t - 2$.
Linearity Property
If $a$ and $b$ are constants while $f(t)$ and $g(t)$ are functions of $t$ whose Laplace transform exists, then
Proof of Linearity Property
$\displaystyle \mathcal{L} \left\{ a \, f(t) + b \, g(t) \right\} = \int_0^\infty e^{-st}\left[ a \, f(t) + b \, g(t) \right] \, dt$
Constant Multiple
If $a$ is a constant and $f(t)$ is a function of $t$, then
Below are some functions $f(t)$ and their Laplace transforms $F(s)$.
| $f(t)$ | $F(s) = \mathcal{L} \left\{f(t)\right\}$ |
| $1$ | $\dfrac{1}{s}$ |
| $t$ | $\dfrac{1}{s^2}$ |
| $t^2$ | $\dfrac{2}{s^3}$ |
| ... | ... |
Recent comments