Problem 13 | Separation of Variables
Problem 13
$xy^3 \, dx + e^{x^2} \, dy = 0$
- Read more about Problem 13 | Separation of Variables
- Log in to post comments
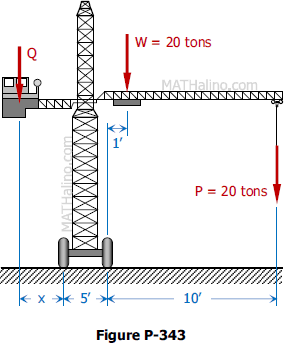
Problem 343 | Equilibrium of Parallel Force System
Problem 343
The weight W of a traveling crane is 20 tons acting as shown in Fig. P-343. To prevent the crane from tipping to the right when carrying a load P of 20 tons, a counterweight Q is used. Determine the value and position of Q so that the crane will remain in equilibrium both when the maximum load P is applied and when the load P is removed.
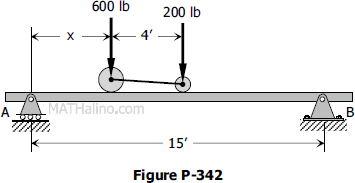
Problem 342 | Equilibrium of Parallel Force System
Problem 342
The wheel loads on a jeep are given in Fig. P-342. Determine the distance x so that the reaction of the beam at A is twice as great as the reaction at B.
Problem 11 | Separation of Variables
Problem 11
$(1 - x)y' = y^2$
Solution 11
Click here to expand or collapse this section
- Read more about Problem 11 | Separation of Variables
- Log in to post comments
Problem 10 | Separation of Variables
Problem 10
$v (dv / dx) = g$, when $x = x_o$, $v = v_o$.
- Read more about Problem 10 | Separation of Variables
- Log in to post comments
Problem 09 | Separation of Variables
Problem 09
$(2a^2 - r^2) \, dr = r^3 \sin \theta \, d\theta$, when $\theta = 0$, $r = a$.
Solution 09
Click here to expand or collapse this section
$\dfrac{(2a^2 - r^2) \, dr}{r^3} = \sin \theta \, d\theta$
- Read more about Problem 09 | Separation of Variables
- Log in to post comments
Problem 07 | Separation of Variables
Problem 07
$y' = x \exp (y - x^2)$, when $x = 0$, $y = 0$.
Solution 07
Click here to expand or collapse this section
$\dfrac{dy}{dx} = x e^{y - x^2}$
- Read more about Problem 07 | Separation of Variables
- Log in to post comments

Recent comments
(…