Situation
The solid pole shown in the figure is loaded with a vertical load P = 25 kN and lateral load H = 0.95 kN. The pole is 3 m high, 300 mm diameter and weighs 22 kN/m³.
 

Problem
The area of a park on a map is 600 mm². If the scale of the map is 1 to 40,000 determine the true area of the park in hectares (1 hectare = 10⁴ m²).

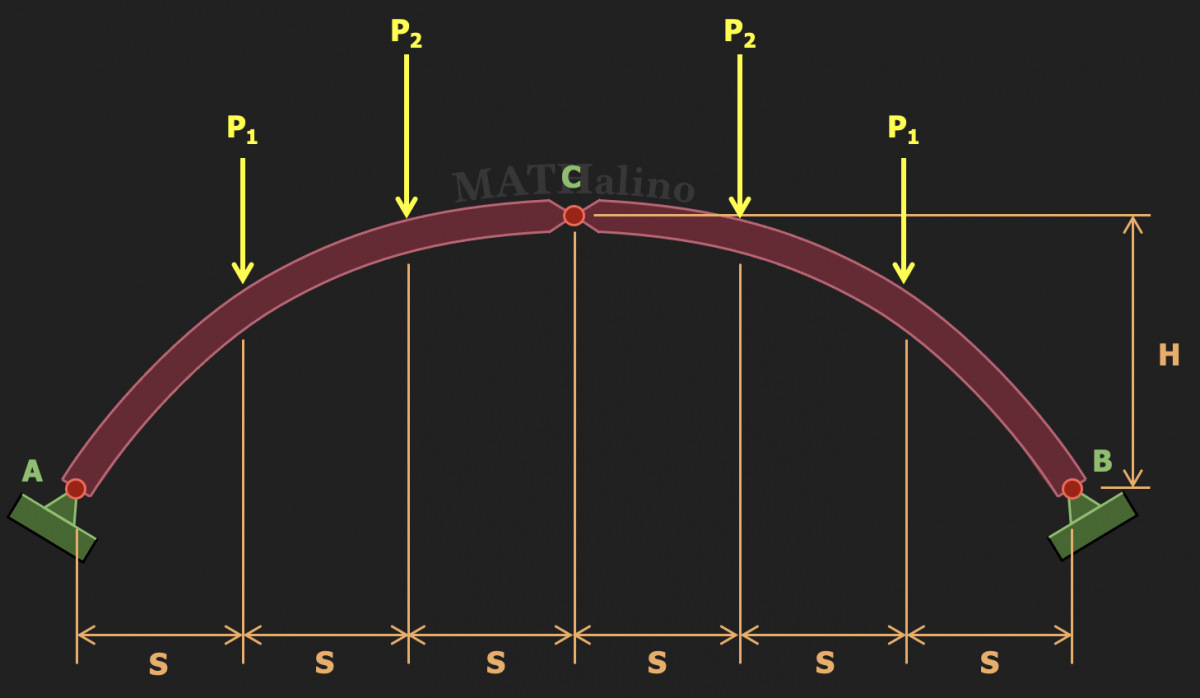
Situation
The three-hinged arch shown below is loaded with symmetrically placed concentrated loads as shown in the figure below.
 

The loads are as follows:
$$P_1 = 90 ~ \text{kN} \qquad P_2 = 240 ~ \text{kN}$$
 

The dimensions are:
$$H = 8 ~ \text{m} \qquad S = 4 ~ \text{kN}$$
 

Calculate the following:
 

1.   The horizontal reaction at A.

2.   The total reaction at B.

3.   The vertical reaction at C.

Problem
Evaluate $\displaystyle \int_0^1 \dfrac{x \, dx}{x^2 + 2}$.

Problem
Determine the radius of curvature of the curve $x = y^3$ at point (1, 1).

Problem
Calculate the area enclosed by the curve $x^2 + y^2 - 10x + 4y - 196 = 0$.

Problem
The first three terms of a geometric progression are 2x, 4x + 14 and 20x - 14. Find the sum of the first ten terms.

Problem
A 50-m steel tape that is is 0.02 m too long was used to measure the distance between two points A and B. If the measured distance was 160.42 m, calculate the correct distance between A and B.

Problem
A circle has an equation of $x^2 + y^2 + 2cy = 0$. Find the value of $c$ when the length of the tangent from (5, 4) to the circle is equal to one.

Problem
Calculate the acute angle between two intersecting surfaces whose equations are as follows:
$$2x - 4y - z = -5$$

$$3x + 4y + 5z = -6$$