Problem
A semi-elliptical arch in a stone bridge has a span of 6 meters and a central height of 2 meters. Find the height of the arch at a distance of 1.5 m from the center of the arch.
| A. 1.41 m | C. 1.56 m |
| B. 1.63 m | D. 1.73 m |
Curvature (symbol, $\kappa$) is the mathematical expression of how much a curve actually curved. It is the measure of the average change in direction of the curve per unit of arc. Imagine a particle to move along the circle from point 1 to point 2, the higher the number of $\kappa$, the more quickly the particle changes in direction. This quick change in direction is apparent in smaller circles.
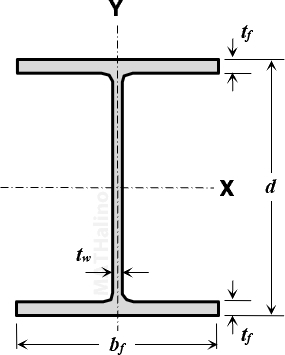
Problem 921
Calculate the sketch the kern of a W360 × 122 section.
Problem
The formula $v = \sqrt{2gh}$ give the velocity, in feet per second, of an object when it falls h feet accelerated by gravity g, in feet per second squared. If g is approximately 32 feet per second squared, find how far an object has fallen if its velocity is 80 feet per second.
| A. 80 feet | C. 70 feet |
| B. 100 feet | D. 90 feet |
Problem
Earth is approximately 93,000,000.00 miles from the sun, and the Jupiter is approximately 484,000,900.00 miles from the sun. How long would it take a spaceship traveling at 7,500.00 mph to fly from Earth to Jupiter?
| A. 9.0 years | C. 6.0 years |
| B. 5.0 years | D. 3.0 years |
Problem
A meteorologist is inflating a spherical balloon with a helium gas. If the radius of a balloon is changing at a rate of 1.5 cm/sec., express the volume V of the balloon as a function of time t (in seconds). Hint: Use composite function relationship Vsphere = 4/3 πr3 as a function of x (radius), and x (radius) as a function of t (time).
| A. V(t) = 5/2 πt3 | C. V(t) = 9/2 πt3 |
| B. V(t) = 7/2 πt3 | D. V(t) = 3/2 πt3 |
Problem
A farmer owned a square field measuring exactly 2261 m on each side. 1898 m from one corner and 1009 m from an adjacent corner stands Narra tree. A neighbor offered to purchase a triangular portion of the field stipulating that a fence should be erected in a straight line from one side of the field to an adjacent side so that the Narra tree was part of the fence. The farmer accepted the offer but made sure that the triangular portion was a minimum area. What was the area of the field the neighbor received and how long was the fence? Hint: Use the Cosine Law.
| A. A = 972,325 m2 and L = 2,236 m |
| B. A = 950,160 m2 and L = 2,122 m |
| C. A = 946,350 m2 and L = 2,495 m |
| D. A = 939,120 m2 and L = 2,018 m |
Problem 920
A compressive load P = 100 kN is applied, as shown in Fig. 9-8a, at a point 70 mm to the left and 30 mm above the centroid of a rectangular section for which h = 300 mm and b = 250 mm. What additional load, acting normal to the cross section at its centroid, will eliminate tensile stress anywhere over the cross section?
Problem 919
From the data in Prob. 918, what additional load applied at the centroid is necessary so that no tensile stress will exist anywhere on the cross-section?
Solution 919
Recent comments
is it not…