Eccentrically Loaded Short Compression Member
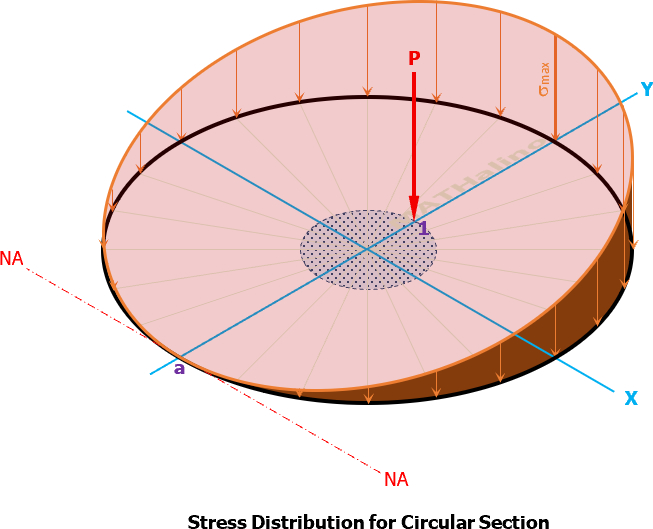
Consider the cross-section below. A compressive load P is applied at any point (ex, ey) with respect to the principal axes x and y. The moment of P about these axes are respectively
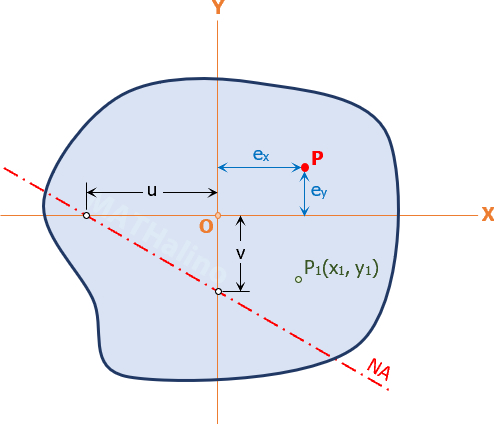
The stress at any point P1(x1, y1) of the cross-section is
Set σ1 = 0 to determine the line of zero stress in the cross section. This line is the neutral axis NA.
Note: r = radius of gyration
$0 = -\dfrac{P}{A} \pm \dfrac{(Pe_y)y}{A{r_x}^2} \pm \dfrac{(Pe_x)x}{A{r_y}^2}$
Which will reduce to a straight line with the following equation
$-1 \pm \dfrac{e_y}{{r_x}^2} \, y \pm \dfrac{e_x}{{r_y}^2} \, x = 0$
Rearrange,
The x- and y-intercepts of this line, which are called u and v from the figure above, are as follows
$\pm \left( \dfrac{e_x}{{r_y}^2}\right)u - 1 = 0$
$u = \pm \dfrac{{r_y}^2}{e_x}$
For y-intercept of NA, set x = 0 and y = v
$\pm \left( \dfrac{e_y}{{r_x}^2}\right)v - 1 = 0$
$v = \pm \dfrac{{r_x}^2}{e_y}$
The NA passes through the quadrant that is opposite to the quadrant containing P, and in general, it is not perpendicular to the direction OP.
Kern of a Section
The location of compressive load P causes the region, hatched with green dotted lines, to be in tensile stress. P2 is a point in this region, hence, the stress at P2 is tension. P1 on the other hand is within the compression region, filled with blue dots. These two regions (compression and tension regions) are separated by the neutral axis, NA.
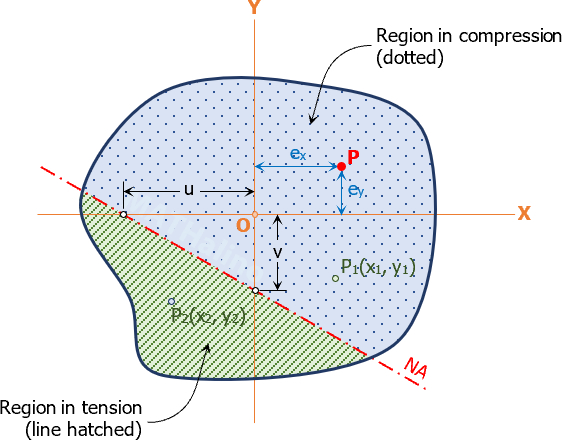
There is a location of compressive force P in the section so that P won’t produce any tensile stress anywhere in the section. The extremities of such location will enclose an area called the kern of the section.
When a compressive force will act at any point in the kern area, the direct compressive stress equals or exceeds the maximum flexural tensile stress at any point in the section. Hence, the whole section is subjected to pure compression.
Kern Area of Rectangular Section
In the case of rectangular section, the extremities of the kern area can be determined by allowing the NA to pass through one corner of the rectangle so that the stress at the corner containing the NA is zero.
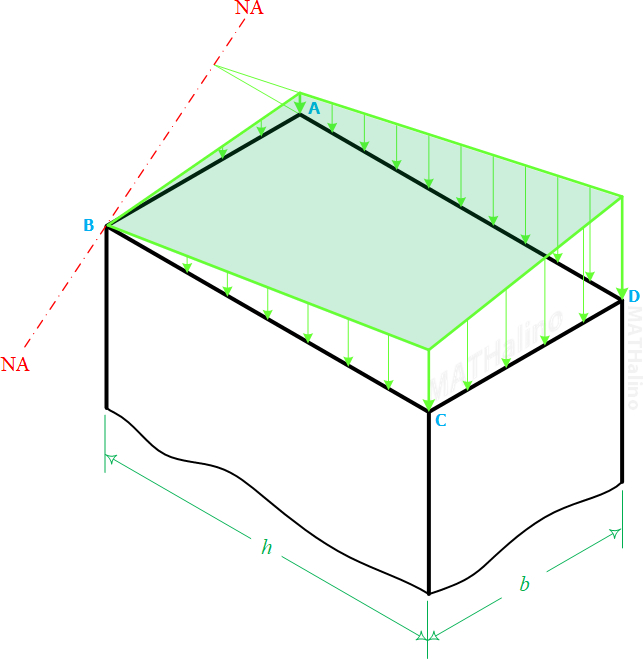
From the figure below, ab is the locus of points of application of P for which corner B has zero stress. Similarly, cd is the locus of loads that cause zero stress at corner C. The hatched region in diamond shape is the kern region.
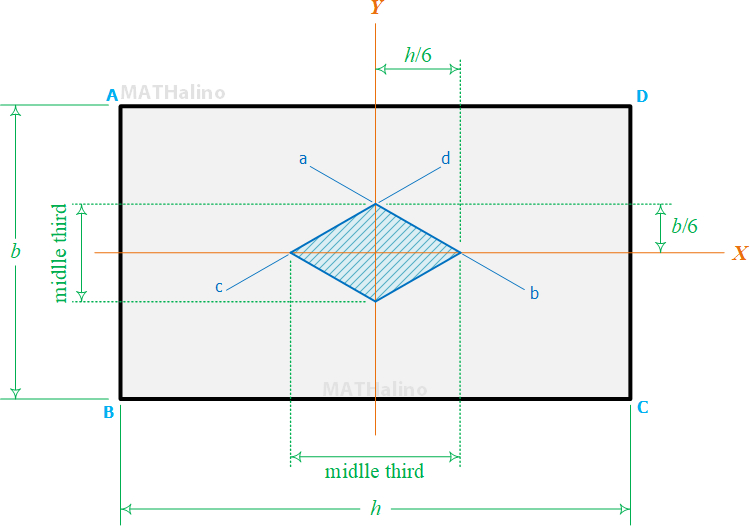
For the equation of the extremities of the kern area, set σ = 0 at (x, y) = (h/2, b/2).
$0 = -\dfrac{P}{bh} \pm \dfrac{(Pe_y)(b/2)}{hb^3 / 12} \pm \dfrac{(Pe_x)(h/2)}{bh^3 / 12}$
$0 = -1 \pm \dfrac{e_y}{b/6} \pm \dfrac{e_x}{h/6}$
This is the equation of the line in intercept form, coordinates are the following: (h/6, 0), (-h/6, 0), (0, b/6), and (0, -b/6).
Back to top
Kern Area of Circular Section
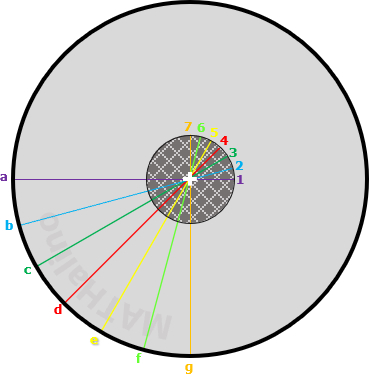
Position P at 1 so that the σa = 0. In the same manner, when P is at 2, 3, 4, ..., 7, the respective stresses σb, σc, σd, ..., σg are zero if P is of the same radial distance as 1. The kern area, therefore is a circle and for its radius:
You can always orient the xy-plane so that the force P is directly on the y-axis, hence, My = 0.
$0 = -\dfrac{P}{\pi r^2} \pm \dfrac{(Pe_y)y}{\pi r^4 / 4} \pm 0$
From the figure below, assign NA to pass through a, so that when force P is at 1 which is at distance ey from the origin, the stress at a is zero.
$0 = -\dfrac{P}{\pi r^2} \pm \dfrac{(Pe_y)(-r)}{\pi r^4 / 4}$
$0 = -1 \mp \dfrac{e_y}{r/4}$
$\mp \dfrac{e_y}{r/4} = 1$
$e_y = \pm r/4$
- Log in to post comments
