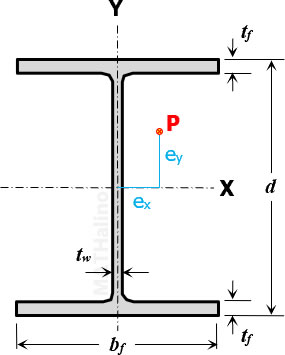
Properties of W360 × 122
A = 15,500 mm2
d = 363 mm
bf = 257 mm
Ix = 365 × 106 mm4
Iy = 61.5 × 106 mm4
tf = 21.7 mm
tw = 13 mm
$0 = -\dfrac{P}{A} \pm \dfrac{M_x y}{I_x} \pm \dfrac{M_y x}{I_y}$
$0 = -\dfrac{P}{A} \pm \dfrac{(Pe_y)(d/2)}{I_x} \pm \dfrac{(Pe_x)(b_f/2)}{I_y}$
$0 = -\dfrac{1}{A} \pm \dfrac{e_y d}{2I_x} \pm \dfrac{e_x b_f}{2I_y}$
$\pm \dfrac{e_y d}{2I_x} \pm \dfrac{e_x b_f}{2I_y} = \dfrac{1}{A}$
$\pm \dfrac{e_y (363)}{2(365 \times 10^6)} \pm \dfrac{e_x (257)}{2(61.5 \times 10^6)} = \dfrac{1}{15,500}$
For x-intercept, set ey = 0
$\pm \dfrac{e_x (257)}{2(61.5 \times 10^6)} = \dfrac{1}{15,500}$
$e_x = \pm 30.9 ~ \text{mm}$
For y-intercept, set ex = 0
$\pm \dfrac{e_y (363)}{2(365 \times 10^6)} = \dfrac{1}{15,500}$
$e_y = 129.7 ~ \text{mm}$
