Combined Axial and Bending

Combined axial compression and bending
$$\sigma = -\dfrac{P}{A} \pm \dfrac{Mc}{I}$$
 

Combined axial tension and bending
$$\sigma = \dfrac{P}{A} \pm \dfrac{Mc}{I}$$
 

For the flexure quantity $Mc/I$, use (+) for fibers in tension and (-) for fibers in compression.
 

Problem 902
Compare the maximum stress in bent rod 1/2 in. square, where the load P is 1/2 in. off center as shown in Figure P-902, with the maximum stress if the rod were straight and the load applied axially.
 

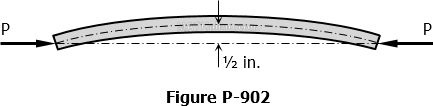
Solution 902
For P applied off-center:

For P applied axially:

$\text{Ratio} = \dfrac{-28P}{-4P}$

$\text{Ratio} = \dfrac{7}{1}$       answer