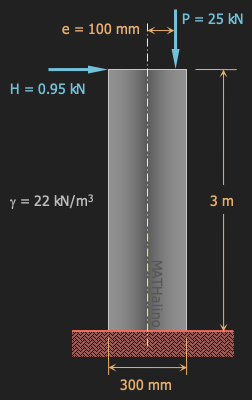
Combined Stresses
Problem 920 | Additional Centroidal Load to Eliminate Tensile Stress Anywhere Over the Cross Section
Problem 920
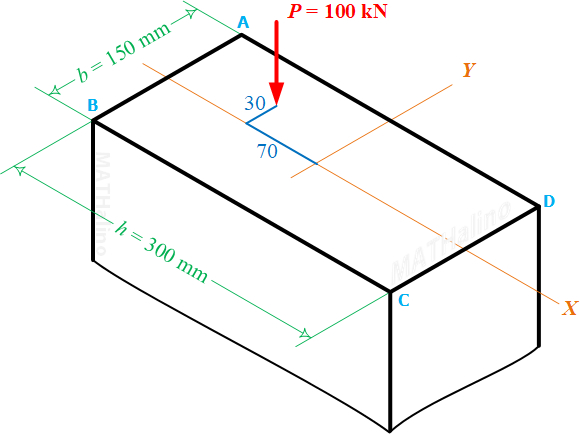
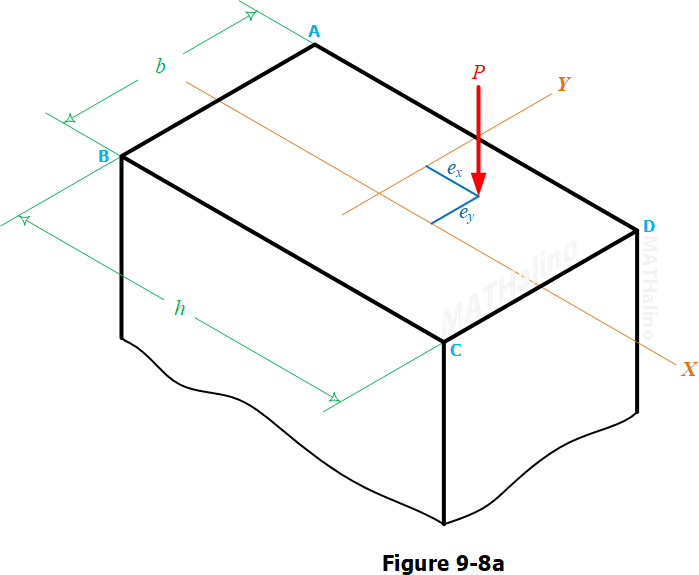
A compressive load P = 100 kN is applied, as shown in Fig. 9-8a, at a point 70 mm to the left and 30 mm above the centroid of a rectangular section for which h = 300 mm and b = 250 mm. What additional load, acting normal to the cross section at its centroid, will eliminate tensile stress anywhere over the cross section?
Problem 919 | Additional Axial Compression Load for the Section to Carry No Tensile Stress
Problem 919
From the data in Prob. 918, what additional load applied at the centroid is necessary so that no tensile stress will exist anywhere on the cross-section?
Solution 919
Problem 918 | Stress at Each Corner of Eccentrically Loaded Rectangular Section
Problem 918
A compressive load P = 12 kips is applied, as in Fig. 9-8a, at a point 1 in. to the right and 2 in. above the centroid of a rectangular section for which h = 10 in. and b = 6 in. Compute the stress at each corner and the location of the neutral axis. Illustrate the answers with a sketch.
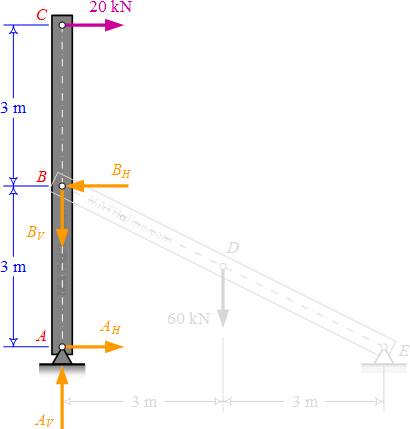
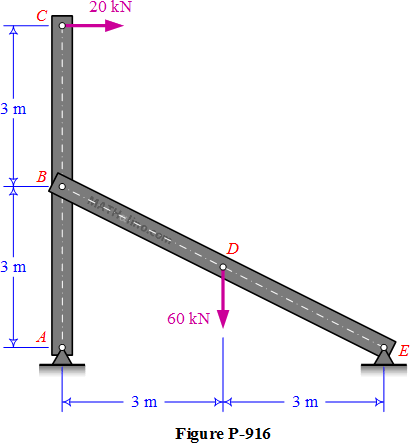
Problem 917 | Combined Axial and Bending
Problem 917
For the structure in Problem 916, calculate the maximum compressive stress in bar ABC if its cross section is 200 mm square.
- Read more about Problem 917 | Combined Axial and Bending
- Log in to post comments
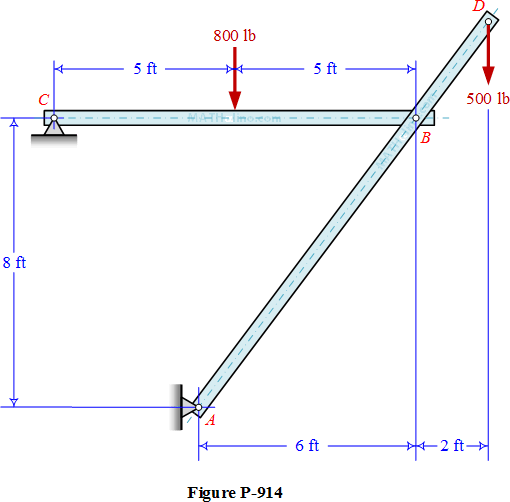
Problem 915 | Combined Axial and Bending
Problem 915
For the structure in Problem 914, compute the maximum tensile stress developed in bar CB.
- Read more about Problem 915 | Combined Axial and Bending
- Log in to post comments