Solution to Problem 217 Axial Deformation
Problem 217
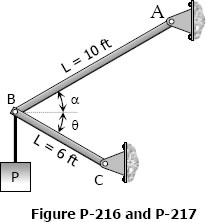
Solve Prob. 216 if rod AB is of steel, with E = 29 × 106 psi. Assume α = 45° and θ = 30°; all other data remain unchanged.
- Read more about Solution to Problem 217 Axial Deformation
- Log in to post comments
Solution to Problem 216 Axial Deformation
Problem 216
As shown in Fig. P-216, two aluminum rods AB and BC, hinged to rigid supports, are pinned together at B to carry a vertical load P = 6000 lb. If each rod has a cross-sectional area of 0.60 in.2 and E = 10 × 106 psi, compute the elongation of each rod and the horizontal and vertical displacements of point B. Assume α = 30° and θ = 30°.
- Read more about Solution to Problem 216 Axial Deformation
- Log in to post comments
Solution to Problem 215 Axial Deformation
Problem 215
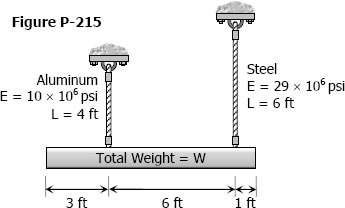
A uniform concrete slab of total weight W is to be attached, as shown in Fig. P-215, to two rods whose lower ends are on the same level. Determine the ratio of the areas of the rods so that the slab will remain level.
Solution 215
Solution to Problem 214 Axial Deformation
Problem 214
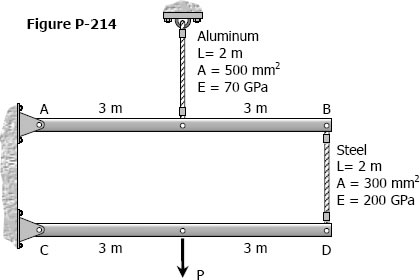
The rigid bars AB and CD shown in Fig. P-214 are supported by pins at A and C and the two rods. Determine the maximum force P that can be applied as shown if its vertical movement is limited to 5 mm. Neglect the weights of all members.
- Read more about Solution to Problem 214 Axial Deformation
- Log in to post comments
Solution to Problem 213 Axial Deformation
Problem 213
The rigid bar AB, attached to two vertical rods as shown in Fig. P-213, is horizontal before the load P is applied. Determine the vertical movement of P if its magnitude is 50 kN.

- Read more about Solution to Problem 213 Axial Deformation
- Log in to post comments
Solution to Problem 211 Axial Deformation
Problem 211
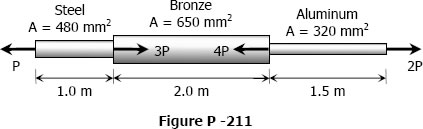
A bronze bar is fastened between a steel bar and an aluminum bar as shown in Fig. p-211. Axial loads are applied at the positions indicated. Find the largest value of P that will not exceed an overall deformation of 3.0 mm, or the following stresses: 140 MPa in the steel, 120 MPa in the bronze, and 80 MPa in the aluminum. Assume that the assembly is suitably braced to prevent buckling. Use Est = 200 GPa, Eal = 70 GPa, and Ebr = 83 GPa.
- Read more about Solution to Problem 211 Axial Deformation
- Log in to post comments
Solution to Problem 208 Axial Deformation
Problem 208
A steel tire, 10 mm thick, 80 mm wide, and 1500.0 mm inside diameter, is heated and shrunk onto a steel wheel 1500.5 mm in diameter. If the coefficient of static friction is 0.30, what torque is required to twist the tire relative to the wheel? Neglect the deformation of the wheel. Use E = 200 GPa.
- Read more about Solution to Problem 208 Axial Deformation
- Log in to post comments

Recent comments
(…