Problem 253
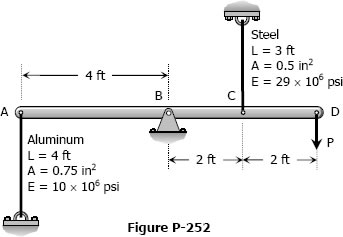
As shown in Fig. P-253, a rigid beam with negligible weight is pinned at one end and attached to two vertical rods. The beam was initially horizontal before the load W = 50 kips was applied. Find the vertical movement of W.
 

Problem 252
The light rigid bar ABCD shown in Fig. P-252 is pinned at B and connected to two vertical rods. Assuming that the bar was initially horizontal and the rods stress-free, determine the stress in each rod after the load after the load P = 20 kips is applied.
 

Problem 251
The two vertical rods attached to the light rigid bar in Fig. P-251 are identical except for length. Before the load W was attached, the bar was horizontal and the rods were stress-free. Determine the load in each rod if W = 6600 lb.
 

Problem 250
In the assembly of the bronze tube and steel bolt shown in Fig. P-250, the pitch of the bolt thread is p = 1/32 in.; the cross-sectional area of the bronze tube is 1.5 in.² and of steel bolt is 3/4 in.² The nut is turned until there is a compressive stress of 4000 psi in the bronze tube. Find the stresses if the nut is given one additional turn. How many turns of the nut will reduce these stresses to zero? Use E_br = 12 × 10⁶ psi and E_st = 29 × 10⁶ psi.
 

Problem 249
There is a radial clearance of 0.05 mm when a steel tube is placed over an aluminum tube. The inside diameter of the aluminum tube is 120 mm, and the wall thickness of each tube is 2.5 mm. Compute the contact pressure and tangential stress in each tube when the aluminum tube is subjected to an internal pressure of 5.0 MPa.
 

Problem 248
Solve Problem 247 if the right wall yields 0.80 mm.
 

Problem 247
The composite bar in Fig. P-247 is stress-free before the axial loads P₁ and P₂ are applied. Assuming that the walls are rigid, calculate the stress in each material if P₁ = 150 kN and P₂ = 90 kN.
 

Problem 246
Referring to the composite bar in Problem 245, what maximum axial load P can be applied if the allowable stresses are 10 ksi for aluminum and 18 ksi for steel.
 

Problem 245
The composite bar in Fig. P-245 is firmly attached to unyielding supports. Compute the stress in each material caused by the application of the axial load P = 50 kips.
 

Problem 244
A homogeneous bar with a cross sectional area of 500 mm² is attached to rigid supports. It carries the axial loads P₁ = 25 kN and P₂ = 50 kN, applied as shown in Fig. P-244. Determine the stress in segment BC. (Hint: Use the results of Prob. 243, and compute the reactions caused by P₁ and P₂ acting separately. Then use the principle of superposition to compute the reactions when both loads are applied.)