315 Power Applied and Removed at Shaft Gears
Problem 315
A 5-m steel shaft rotating at 2 Hz has 70 kW applied at a gear that is 2 m from the left end where 20 kW are removed. At the right end, 30 kW are removed and another 20 kW leaves the shaft at 1.5 m from the right end. (a) Find the uniform shaft diameter so that the shearing stress will not exceed 60 MPa. (b) If a uniform shaft diameter of 100 mm is specified, determine the angle by which one end of the shaft lags behind the other end. Use G = 83 GPa.
- Read more about 315 Power Applied and Removed at Shaft Gears
- Log in or register to post comments
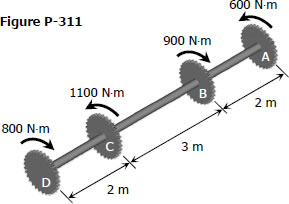
314 Maximum Shear and Relative Gear Rotation of a Compound Steel Shaft
Problem 314
The steel shaft shown in Fig. P-314 rotates at 4 Hz with 35 kW taken off at A, 20 kW removed at B, and 55 kW applied at C. Using G = 83 GPa, find the maximum shearing stress and the angle of rotation of gear A relative to gear C.
313 Maximum Torque That Can be Applied to a Hollow Steel Shaft
Problem 313
Determine the maximum torque that can be applied to a hollow circular steel shaft of 100-mm outside diameter and an 80-mm inside diameter without exceeding a shearing stress of 60 MPa or a twist of 0.5 deg/m. Use G = 83 GPa.
312 Deformation of Flexible Shaft Made From Steel Wire Encased in Stationary Tube
Problem 312
A flexible shaft consists of a 0.20-in-diameter steel wire encased in a stationary tube that fits closely enough to impose a frictional torque of 0.50 lb·in/in. Determine the maximum length of the shaft if the shearing stress is not to exceed 20 ksi. What will be the angular deformation of one end relative to the other end? G = 12 × 106 psi.
310 Strength Comparison of Hollow and Solid Steel Shafts of Equal Outside Diameters
Problem 310
Show that the hollow circular shaft whose inner diameter is half the outer diameter has a torsional strength equal to 15/16 of that of a solid shaft of the same outside diameter.
309 Finding the Diameter of a Propeller Shaft Transmitting a Power
Problem 309
A steel propeller shaft is to transmit 4.5 MW at 3 Hz without exceeding a shearing stress of 50 MPa or twisting through more than 1° in a length of 26 diameters. Compute the proper diameter if G = 83 GPa.
308 Maximum Horsepower That Can be Transmitted by Steel Shaft
Problem 308
A 2-in-diameter steel shaft rotates at 240 rpm. If the shearing stress is limited to 12 ksi, determine the maximum horsepower that can be transmitted.
307 Power Transmitted by Solid Steel Shaft of Unknown Diameter
Problem 307
A solid steel shaft 5 m long is stressed at 80 MPa when twisted through 4°. Using G = 83 GPa, compute the shaft diameter. What power can be transmitted by the shaft at 20 Hz?
306 Maximum Shearing Stress of Marine Propeller Shaft
Problem 306
A steel marine propeller shaft 14 in. in diameter and 18 ft long is used to transmit 5000 hp at 189 rpm. If G = 12 × 106 psi, determine the maximum shearing stress.
- Read more about 306 Maximum Shearing Stress of Marine Propeller Shaft
- Log in or register to post comments

Recent comments