Shear and Moment Diagrams
Shear and Moment Diagrams
Consider a simple beam shown of length L that carries a uniform load of w (N/m) throughout its length and is held in equilibrium by reactions R1 and R2. Assume that the beam is cut at point C a distance of x from he left support and the portion of the beam to the right of C be removed. The portion removed must then be replaced by vertical shearing force V together with a couple M to hold the left portion of the bar in equilibrium under the action of R1 and wx.
- Read more about Shear and Moment Diagrams
- Log in or register to post comments
Shear and Moment in Beams
Definition of a Beam
A beam is a bar subject to forces or couples that lie in a plane containing the longitudinal section of the bar. According to determinacy, a beam may be determinate or indeterminate.
Statically Determinate Beams
Statically determinate beams are those beams in which the reactions of the supports may be determined by the use of the equations of static equilibrium. The beams shown below are examples of statically determinate beams.
- Read more about Shear and Moment in Beams
- Log in or register to post comments
Solution to Problem 350 | Helical Springs
Problem 350
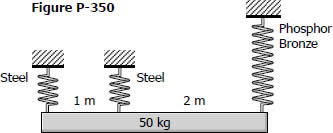
As shown in Fig. P-350, a homogeneous 50-kg rigid block is suspended by the three springs whose lower ends were originally at the same level. Each steel spring has 24 turns of 10-mm-diameter on a mean diameter of 100 mm, and G = 83 GPa. The bronze spring has 48 turns of 20-mm-diameter wire on a mean diameter of 150 mm, and G = 42 GPa. Compute the maximum shearing stress in each spring using Eq. (3-9).
- Read more about Solution to Problem 350 | Helical Springs
- Log in or register to post comments
Solution to Problem 349 | Helical Springs
Problem 349
A rigid bar, hinged at one end, is supported by two identical springs as shown in Fig. P-349. Each spring consists of 20 turns of 10-mm wire having a mean diameter of 150 mm. Compute the maximum shearing stress in the springs, using Eq. (3-9). Neglect the mass of the rigid bar.
- Read more about Solution to Problem 349 | Helical Springs
- Log in or register to post comments
Solution to Problem 348 | Helical Springs
Problem 348
A rigid bar, pinned at O, is supported by two identical springs as shown in Fig. P-348. Each spring consists of 20 turns of 3/4-in-diameter wire having a mean diameter of 6 in. Determine the maximum load W that may be supported if the shearing stress in the springs is limited to 20 ksi. Use Eq. (3-9).
- Read more about Solution to Problem 348 | Helical Springs
- 1 comment
- Log in or register to post comments
Solution to Problem 347 | Helical Springs
Problem 347
Two steel springs arranged in series as shown in Fig. P-347 supports a load P. The upper spring has 12 turns of 25-mm-diameter wire on a mean radius of 100 mm. The lower spring consists of 10 turns of 20-mm diameter wire on a mean radius of 75 mm. If the maximum shearing stress in either spring must not exceed 200 MPa, compute the maximum value of P and the total elongation of the assembly. Use Eq. (3-10) and G = 83 GPa. Compute the equivalent spring constant by dividing the load by the total elongation.
- Read more about Solution to Problem 347 | Helical Springs
- Log in or register to post comments
Solution to Problem 346 | Helical Springs
Problem 346
Compute the maximum shearing stress developed in a phosphor bronze spring having mean diameter of 200 mm and consisting of 24 turns of 20-mm diameter wire when the spring is stretched 100 mm. Use Eq. (3-10) and G = 42 GPa.
- Read more about Solution to Problem 346 | Helical Springs
- 1 comment
- Log in or register to post comments

Recent comments