$\tau_{max} = \dfrac{16PR}{\pi d^3} \left( \dfrac{4m - 1}{4m - 4} + \dfrac{0.615}{m} \right)$ → Equation (3-10)
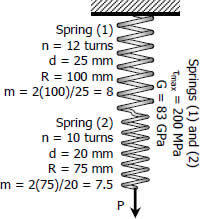For Spring (1)
$200 = \dfrac{16P(100)}{\pi (25^3)} \left[ \dfrac{4(8) - 1}{4(8) - 4} + \dfrac{0.615}{8} \right]$
$P = 5182.29 \, \text{N}$
For Spring (2)
$200 = \dfrac{16P(75)}{\pi (20^3)} \left[ \dfrac{4(7.5) - 1}{4(7.5) - 4} + \dfrac{0.615}{7.5} \right]$
$P = 3498.28 \, \text{N}$
Use
$P = 3498.28 \, \text{ N}$ answer
Total elongation:
$\delta = \delta_1 + \delta_2$
$\delta = \left( \dfrac{64PR^3n}{Gd^4} \right)_1 + \left( \dfrac{64PR^3n}{Gd^4} \right)_2$
$\delta = \dfrac{64(3498.28)(100^3)12}{83\,000(25^4)} + \dfrac{64(3498.28)(75^3)10}{83\,000(20^4)}$
$\delta = 153.99 \, \text{ mm}$ answer
Equivalent spring constant, kequivalent:
$k_{equivalent} = \dfrac{P}{\delta} = \dfrac{3498.28}{153.99}$
$k_{equivalent} = 22.72 \, \text{N/mm}$ answer
