Helical Springs
When close-coiled helical spring, composed of a wire of round rod of diameter d wound into a helix of mean radius R with n number of turns, is subjected to an axial load P produces the following stresses and elongation:
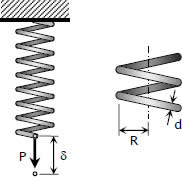
The maximum shearing stress is the sum of the direct shearing stress τ1 = P/A and the torsional shearing stress τ2 = Tr/J, with T = PR.
$\tau = \tau_1 + \tau_2$
$\tau = \dfrac{P}{\pi d^2 / 4} + \dfrac{16PR}{\pi d^3}$
This formula neglects the curvature of the spring. This is used for light spring where the ratio d/4R is small.
For heavy springs and considering the curvature of the spring, A.M. Wahl formula a more precise, it is given by:
where m is called the spring index and (4m - 1)/(4m - 4) is the Wahl Factor.
The elongation of the bar is
Notice that the deformation δ is directly proportional to the applied load P. The ratio of P to δ is called the spring constant k and is equal to
Springs in Series
For two or more springs with spring laid in series, the resulting spring constant k is given by
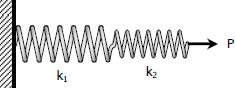
where k1, k2,... are the spring constants for different springs.
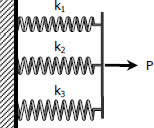
Springs in Parallel
For two or more springs in parallel, the resulting spring constant is
