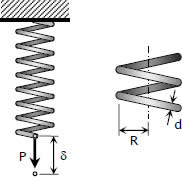
Helical Springs
When close-coiled helical spring, composed of a wire of round rod of diameter d wound into a helix of mean radius R with n number of turns, is subjected to an axial load P produces the following stresses and elongation:
The maximum shearing stress is the sum of the direct shearing stress τ1 = P/A and the torsional shearing stress τ2 = Tr/J, with T = PR.
- Read more about Helical Springs
- Log in to post comments