TORSION

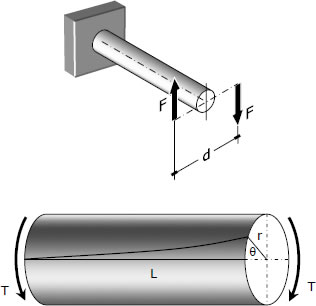
Consider a bar to be rigidly attached at one end and twisted at the other end by a torque or twisting moment T equivalent to F × d, which is applied perpendicular to the axis of the bar, as shown in the figure. Such a bar is said to be in torsion.

TORSIONAL SHEARING STRESS, τ

For a solid or hollow circular shaft subject to a twisting moment T, the torsional shearing stress τ at a distance ρ from the center of the shaft is

where J is the polar moment of inertia of the section and r is the outer radius.

For solid cylindrical shaft:

J = \dfrac{\pi}{32} D^4

\tau_{max} = \dfrac{16T}{\pi D^3}

For hollow cylindrical shaft:

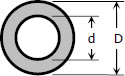J = \dfrac{\pi}{32}(D^4 - d^4)

\tau_{max} = \dfrac{16TD}{\pi(D^4 - d^4)}

ANGLE OF TWIST

The angle θ through which the bar length L will twist is

where T is the torque in N·mm, L is the length of shaft in mm, G is shear modulus in MPa, J is the polar moment of inertia in mm⁴, D and d are diameter in mm, and r is the radius in mm.

POWER TRANSMITTED BY THE SHAFT

A shaft rotating with a constant angular velocity ω (in radians per second) is being acted by a twisting moment T. The power transmitted by the shaft is

where T is the torque in N·m, f is the number of revolutions per second, and P is the power in watts.