$T = 2At\tau$
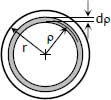Where:
$T = dT; \,\, A = \pi \rho^2; \,\, t = d\rho$
$\dfrac{\tau}{\rho} = \dfrac{\tau_{max}}{r}; \,\, \tau = \dfrac{\tau_{max}}{\rho}$
$dT = 2\pi(\rho^2) d\rho \left( \dfrac{\tau_{max}\rho}{r} \right)$
$T = \dfrac{2\pi \tau_{max}}{r} {\displaystyle \int_0^{\,r}} \rho^3 \, d\rho$
$T = \dfrac{2\pi \tau_{max}}{r} \left[ \dfrac{\rho^4}{4} \right]_0^r$
$T = \dfrac{2\pi \tau_{max}}{r} \left( \dfrac{r^4}{4} \right)$
$T = \dfrac{\tau_{max}}{r} \left( \dfrac{\pi r^4}{2} \right)$
$T = \dfrac{\tau_{max}}{r} J$
$\tau_{max} = \dfrac{Tr}{J}$ and it follows that $\tau_{max} = \dfrac{T\rho}{J}$ (okay!)
