Solution to Problem 343 | Helical Springs
Problem 343
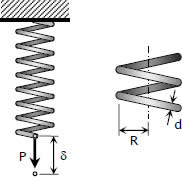
Determine the maximum shearing stress and elongation in a helical steel spring composed of 20 turns of 20-mm-diameter wire on a mean radius of 90 mm when the spring is supporting a load of 1.5 kN. Use Eq. (3-10) and G = 83 GPa.
- Read more about Solution to Problem 343 | Helical Springs
- Log in or register to post comments
Helical Springs
When close-coiled helical spring, composed of a wire of round rod of diameter d wound into a helix of mean radius R with n number of turns, is subjected to an axial load P produces the following stresses and elongation:
The maximum shearing stress is the sum of the direct shearing stress τ1 = P/A and the torsional shearing stress τ2 = Tr/J, with T = PR.
- Read more about Helical Springs
- Log in or register to post comments
Solution to Problem 341 | Torsion of thin-walled tube
Problem 341
Derive the torsion formula τ = Tρ / J for a solid circular section by assuming the section is composed of a series of concentric thin circular tubes. Assume that the shearing stress at any point is proportional to its radial distance.
- Read more about Solution to Problem 341 | Torsion of thin-walled tube
- Log in or register to post comments
Solution to Problem 340 | Torsion of thin-walled tube
Problem 340
A tube 2 mm thick has the shape shown in Fig. P-340. Find the shearing stress caused by a torque of 600 N·m.
- Read more about Solution to Problem 340 | Torsion of thin-walled tube
- Log in or register to post comments
Solution to Problem 339 | Torsion of thin-walled tube
Problem 339
A torque of 450 lb·ft is applied to the square section shown in Fig. P-339. Determine the smallest permissible dimension a if the shearing stress is limited to 6000 psi.
- Read more about Solution to Problem 339 | Torsion of thin-walled tube
- Log in or register to post comments
Solution to Problem 338 | Torsion of thin-walled tube
Problem 338
A tube 0.10 in. thick has an elliptical shape shown in Fig. P-338. What torque will cause a shearing stress of 8000 psi?
- Read more about Solution to Problem 338 | Torsion of thin-walled tube
- Log in or register to post comments
Solution to Problem 337 | Torsion of thin-walled tube
Problem 337
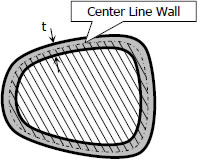
A torque of 600 N·m is applied to the rectangular section shown in Fig. P-337. Determine the wall thickness t so as not to exceed a shear stress of 80 MPa. What is the shear stress in the short sides? Neglect stress concentration at the corners.
- Read more about Solution to Problem 337 | Torsion of thin-walled tube
- Log in or register to post comments
Torsion of thin-walled tube
The torque applied to thin-walled tubes is expressed as
- Read more about Torsion of thin-walled tube
- Log in or register to post comments
Solution to Problem 335 | Flanged bolt couplings
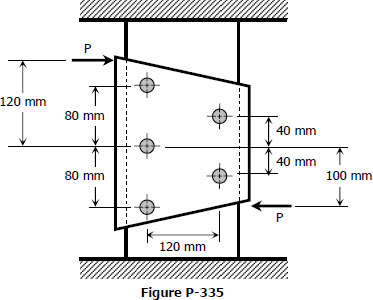
Problem 335
The plate shown in Fig. P-335 is fastened to the fixed member by five 10-mm-diameter rivets. Compute the value of the loads P so that the average shearing stress in any rivet does not exceed 70 MPa. (Hint: Use the results of Prob. 332.)
- Read more about Solution to Problem 335 | Flanged bolt couplings
- Log in or register to post comments
Solution to Problem 334 | Flanged bolt couplings
Problem 334
Six 7/8-in-diameter rivets fasten the plate in Fig. P-334 to the fixed member. Using the results of Prob. 332, determine the average shearing stress caused in each rivet by the 14 kip loads. What additional loads P can be applied before the shearing stress in any rivet exceeds 8000 psi?
- Read more about Solution to Problem 334 | Flanged bolt couplings
- Log in or register to post comments
Recent comments
(…