Solution to Problem 335 | Flanged bolt couplings | Strength of Materials Review at MATHalino

Problem 335
The plate shown in Fig. P-335 is fastened to the fixed member by five 10-mm-diameter rivets. Compute the value of the loads P so that the average shearing stress in any rivet does not exceed 70 MPa. (Hint: Use the results of Prob. 332.)

Solution 335

Click here to expand or collapse this section

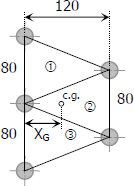
Solving for location of centroid of rivets:

$A X_G = \Sigma ax$

Where
$A = \frac{1}{2}(80 + 160)(120) = 14\,400 \, \text{mm}^2$

$a_1 = a_2 = a_3 = \frac{1}{2}(80)(120) = 4800 \, \text{mm}^2$

$x_1 = x_3 = \frac{1}{3}(120) = 40 \, \text{mm}$

$x_2 = \frac{2}{3}(120) = 80 \, \text{mm}$

$14\,400X_G = 4800(40) + 4800(80) + 4800(40)$

$X_G = \frac{160}{3} \, \text{mm}$

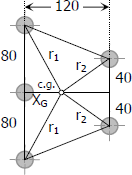$r_1 = \sqrt{(\frac{160}{3})^2 + 80^2} = 96.148 \, \text{mm}$

$r_2 = \sqrt{(120 - \frac{160}{3})^2 + 40^2} = 77.746 \, \text{mm}$

$J = \Sigma A\rho^2 = \frac{1}{4}\pi (10^2)(2r_1^2 + 2r_2^2 + X_G^2)$

$J = \frac{1}{4}\pi (10^2)\, [ \, 2(96.148^2) + 2(77.746^2) + (\frac{160}{3})^2 \, ]$

$J = 2\,624\,973.55 \, \text{mm}^4$

Another way to solve for J

$J = \Sigma A(x^2 + y^2) = \frac{1}{4}\pi (10^2)[ \, 3({X_G}^2) + 2(120 - X_G)^2 + 2(80^2) + 2(40^2) \, ]$

$J = \frac{1}{4}\pi (10^2)[ \, 3(\frac{160}{3})^2 + 2(120 - \frac{160}{3})^2 + 2(80^2) + 2(40^2) \, ]$

$J = 2\,624\,975.19 \, \text{mm}^4$

$T = 120P + 100P = 220P$

The critical rivets are at distance r₁ from centroid:
$\tau = \dfrac{T \rho}{J}$

$\tau_{max} = \dfrac{Tr_1}{J}$

$70 = \dfrac{220P(96.148)}{2\,624\,973.55}$

$P = 8686.8 \, \text{N}$ answer

Solution to Problem 335 | Flanged bolt couplings

Navigation

Recent comments