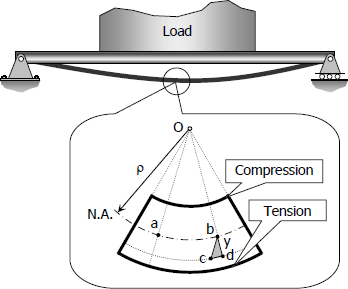
Stresses in Beams

Stresses in Beams
Forces and couples acting on the beam cause bending (flexural stresses) and shearing stresses on any cross section of the beam and deflection perpendicular to the longitudinal axis of the beam. If couples are applied to the ends of the beam and no forces act on it, the bending is said to be pure bending. If forces produce the bending, the bending is called ordinary bending.
 

Moving Loads

Moving Loads
From the previous section, we see that the maximum moment occurs at a point of zero shears. For beams loaded with concentrated loads, the point of zero shears usually occurs under a concentrated load and so the maximum moment.
 

Beams and girders such as in a bridge or an overhead crane are subject to moving concentrated loads, which are at fixed distance with each other. The problem here is to determine the moment under each load when each load is in a position to cause a maximum moment. The largest value of these moments governs the design of the beam.
 

Solution to Problem 441 | Relationship Between Load, Shear, and Moment

Problem 441
A beam ABCD is supported by a roller at A and a hinge at D. It is subjected to the loads shown in Fig. P-441, which act at the ends of the vertical members BE and CF. These vertical members are rigidly attached to the beam at B and C. (Draw shear and moment diagrams for the beam ABCD only.)

 
441-beam-with-vertical-members.gif

 

Solution to Problem 440 | Relationship Between Load, Shear, and Moment

Problem 440
A frame ABCD, with rigid corners at B and C, supports the concentrated load as shown in Fig. P-440. (Draw shear and moment diagrams for each of the three parts of the frame.)

 
440-rigid-frame.gif

 

Solution to Problem 439 | Relationship Between Load, Shear, and Moment

Problem 439
A beam supported on three reactions as shown in Fig. P-439 consists of two segments joined by frictionless hinge at which the bending moment is zero.

 
439-continuous-beam-with-internal-hinge.gif

 

Solution to Problem 438 | Relationship Between Load, Shear, and Moment

Problem 438
The beam loaded as shown in Fig. P-438 consists of two segments joined by a frictionless hinge at which the bending moment is zero.

 
438-hinged-cantilever-beam.gif

 

Solution to Problem 437 | Relationship Between Load, Shear, and Moment

Problem 437
Cantilever beam loaded as shown in Fig. P-437.

 
437-cantilever-beam-uniform-point-loads.gif

 

Solution to Problem 436 | Relationship Between Load, Shear, and Moment

Problem 436
A distributed load is supported by two distributed reactions as shown in Fig. P-436.

 
436-uniform-load-and-reactions.gif

 

Solution to Problem 435 | Relationship Between Load, Shear, and Moment

Problem 435
Beam loaded and supported as shown in Fig. P-435.

 
435-beam-with-uniform-support.gif

 

Solution to Problem 434 | Relationship Between Load, Shear, and Moment

Problem 434
Beam loaded as shown in Fig. P-434.

 
434-overhang-beam-point-moment-and-uniform-loads.gif