Problem 243
A homogeneous rod of constant cross section is attached to unyielding supports. It carries an axial load P applied as shown in Fig. P-243. Prove that the reactions are given by R1 = Pb/L and R2 = Pa/L.
Problem 242
The assembly in Fig. P-242 consists of a light rigid bar AB, pinned at O, that is attached to the steel and aluminum rods. In the position shown, bar AB is horizontal and there is a gap, Δ = 5 mm, between the lower end of the steel rod and its pin support at C. Compute the stress in the aluminum rod when the lower end of the steel rod is attached to its support.
Problem 241
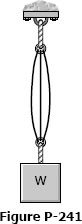As shown in Fig. P-241, three steel wires, each 0.05 in.2 in area, are used to lift a load W = 1500 lb. Their unstressed lengths are 74.98 ft, 74.99 ft, and 75.00 ft.
(a) What stress exists in the longest wire?
(b) Determine the stress in the shortest wire if W = 500 lb.
Problem 240
Three steel eye-bars, each 4 in. by 1 in. in section, are to be assembled by driving rigid 7/8-in.-diameter drift pins through holes drilled in the ends of the bars. The center-line spacing between the holes is 30 ft in the two outer bars, but 0.045 in. shorter in the middle bar. Find the shearing stress developed in the drip pins. Neglect local deformation at the holes.
Problem 239
The rigid platform in Fig. P-239 has negligible mass and rests on two steel bars, each 250.00 mm long. The center bar is aluminum and 249.90 mm long. Compute the stress in the aluminum bar after the center load P = 400 kN has been applied. For each steel bar, the area is 1200 mm2 and E = 200 GPa. For the aluminum bar, the area is 2400 mm2 and E = 70 GPa.
Problem 238
The lower ends of the three bars in Fig. P-238 are at the same level before the uniform rigid block weighing 40 kips is attached. Each steel bar has a length of 3 ft, and area of 1.0 in.2, and E = 29 × 106 psi. For the bronze bar, the area is 1.5 in.2 and E = 12 × 106 psi. Determine (a) the length of the bronze bar so that the load on each steel bar is twice the load on the bronze bar, and (b) the length of the bronze that will make the steel stress twice the bronze stress.
In Problem 236, how should the lengths of the two identical copper rods be changed so that each material will be stressed to its allowable limit?
Problem 236
A rigid block of mass M is supported by three symmetrically spaced rods as shown in Fig. P-236. Each copper rod has an area of 900 mm2; E = 120 GPa; and the allowable stress is 70 MPa. The steel rod has an area of 1200 mm2; E = 200 GPa; and the allowable stress is 140 MPa. Determine the largest mass M which can be supported.
Problem 235
A timber column, 8 in. × 8 in. in cross section, is reinforced on each side by a steel plate 8 in. wide and t in. thick. Determine the thickness t so that the column will support an axial load of 300 kips without exceeding a maximum timber stress of 1200 psi or a maximum steel stress of 20 ksi. The moduli of elasticity are 1.5 × 106 psi for timber, and 29 × 106 psi for steel.
Problem 234
A reinforced concrete column 200 mm in diameter is designed to carry an axial compressive load of 300 kN. Determine the required area of the reinforcing steel if the allowable stresses are 6 MPa and 120 MPa for the concrete and steel, respectively. Use Eco = 14 GPa and Est = 200 GPa.
Recent comments
(…