Solution to Problem 216 Axial Deformation

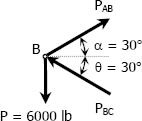
From FBD of Joint B
$\Sigma F_H = 0$

$P_{AB} \cos 30^\circ = P_{BC} \cos 30^\circ$

$P_{AB} = P_{BC}$
 

$\Sigma F_V = 0$

$P_{AB} \sin 30^\circ + P_{BC} \sin 30^\circ = 6000$

$P_{AB} (0.5) + P_{AB} (0.5) = 6000$

$P_{AB} = 6000 \, \text{lb}$ tension

$P_{BC} = 6000 \, \text{lb}$ compression
 

$\delta = \dfrac{PL}{AE}$

$\delta_{AB} = \dfrac{6000(10 \times 12)}{0.6(10 \times 10^6)} = 0.12 \, \text{inch lengthening}$           answer

$\delta_{BC} = \dfrac{6000(6 \times 12)}{0.6(10 \times 10^6)} = 0.072 \, \text{inch shortening}$           answer
 

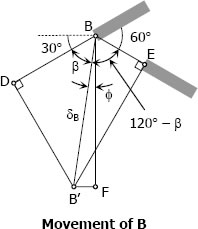From 'Movement of B' diagram:
DB = δ_AB = 0.12 inch
BE = δ_BE = 0.072 inch
δ_B = BB' = displacement of B
B' = final position of $B$ after elongation

Triangle BDB':
$\cos \beta = \dfrac{0.12}{\delta_B}$

$\delta_B = \dfrac{0.12}{\cos \beta}$
 

Triangle BEB':
$\cos (120^\circ - \beta) = \dfrac{0.072}{\delta_B}$

$\delta_B = \dfrac{0.072}{\cos (120^\circ - \beta)}$
 

$\delta_B = \delta_B$

$\dfrac{0.12}{\cos \beta} = \dfrac{0.072}{\cos (120^\circ - \beta)}$

$\dfrac{\cos 120^\circ \, \cos \beta + \sin 120^\circ \, \sin \beta}{\cos \beta} = 0.6$

$-0.5 + \sin 120^\circ \, \tan \beta = 0.6$

$\tan \beta = \dfrac{1.1}{\sin 120^\circ}$

$\beta = 51.79^\circ$
 

$\phi = 90 - (30^\circ + \beta) = 90^\circ - (30^\circ + 51.79^\circ)$

$\phi = 8.21^\circ$

$\delta_B = \dfrac{0.12}{\cos 51.79^\circ}$

$\delta_B = 0.194 \, \text{inch}$
 

Triangle BFB':
$\delta_h = B'F = \delta_B \sin \phi = 0.194 \sin 8.21^\circ$

$\delta_h = 0.0277 \, \text{inch}$

$\delta_h = 0.0023 \, \text{ft}$       → horizontal displacement of B       answer
 

$\delta_v = BF = \delta_B \cos \phi = 0.194 \cos 8.21^\circ$

$\delta_v = 0.192 \, \text{inch}$

$\delta_v = 0.016 \, \text{ft}$       → vertical displacement of B       answer